Question

如图，已知线段AB上一点O，以OB为半径的⊙O交线段AB于C，以线段AO为直径的半圆交⊙O于点D，过点B作AB的垂线与AD相交于点E，
（1）求证：AE切⊙O于D；
（2）求OD•OE的值；
（3）如果⊙O的半径为r，且OD+OE=3r，求OD、OE的长．

Answer 1

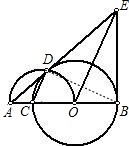解：（1）证明：连接OD
∵AO为半圆直径
∴∠ADO=90°，OD⊥AE，OD为⊙O半径
∴AE切⊙O于D

（2）连接BD
∵BC为直径
∴∠CDB=90°
∵EB⊥AB
∴∠EBA=90°
∴∠CDB=∠EBA
∵EB、ED是⊙O的两切线
∴EB=ED，OE平分∠BED
∴EO⊥BD
∴∠DBC=∠BEO
∴△DCB∽△BOE
∴
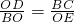
∴OD•OE=BC•BO
∴OD•OE=2r•r=2r²

（3）设以OD、OE为根的方程是x²-3rx+2r²=0（2）
∴x₁=r，x₂=2r
∵OD＜OE
∴OD=r，OE=2r
分析：（1）连接OD，证明OD⊥AE即可．
（2）连接BD，证明△DCB∽△BOE，得出OD•OE=BC•BO，得出结果．
（3）由一元二次方程根与系数的关系，可知OD，OE是方程x²-3rx+2r²=0的两根，解方程求出结果．
点评：综合考查了圆与相似三角形的性质和应用，以及解一元二次方程．连接半径是证明切线常用的辅助线的作法．