题目内容
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求![]() 的面积;
的面积;
(4)在直线![]() 上存在异于点
上存在异于点![]() 的另一个点
的另一个点![]() ,使得
,使得![]() 与
与![]() 的面积相等,求
的面积相等,求![]() 点的坐标.
点的坐标.
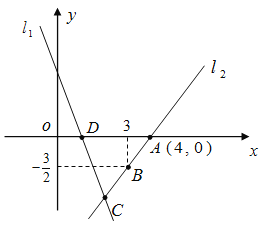
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)P点坐标为(6,3).
;(4)P点坐标为(6,3).
【解析】试题分析:(1)因为点D是一次函数![]() 与x轴的交点,所以令y=0,即可求出点D坐标,
与x轴的交点,所以令y=0,即可求出点D坐标,
(2)设直线![]() 的解析式为:
的解析式为:![]() ,将点A,B坐标代入列二元一次方程组即可求出k,b,即可得
,将点A,B坐标代入列二元一次方程组即可求出k,b,即可得![]() 的解析式,
的解析式,
(3)因为点C是直线![]() 和直线
和直线![]() 的交点,可将两直线所在解析式联立方程组,求出点C坐标,再根据点A,D可得三角形的底边长,由点C的纵坐标可得三角形的高,代入三角形面积公式进行计算即可求解,
的交点,可将两直线所在解析式联立方程组,求出点C坐标,再根据点A,D可得三角形的底边长,由点C的纵坐标可得三角形的高,代入三角形面积公式进行计算即可求解,
(4)根据△![]() 与△
与△![]() 的面积相等,可知点P与点C到x轴的距离相等,且又不同于点C,所以求出点P的纵坐标,然后代入直线
的面积相等,可知点P与点C到x轴的距离相等,且又不同于点C,所以求出点P的纵坐标,然后代入直线![]() 的解析式即可求解.
的解析式即可求解.
试题解析:(1)∵ y=﹣3x+3,
∴令y=0,得﹣3x+3=0,解得x=1,
∴D(1,0),
(2)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0,x=3,y=![]() ,代入表达式y=kx+b,得
,代入表达式y=kx+b,得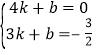 ,解得
,解得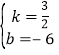 ,所以直线l2的解析表达式为y=
,所以直线l2的解析表达式为y=![]() ,
,
(3)由图象可得: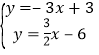 ,解得
,解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ,
,
(4)因为点P与点C到AD的距离相等,所以P点的纵坐标为3,当y=3时,![]() ,解得x=6,所以P点坐标为(6,3).
,解得x=6,所以P点坐标为(6,3).

【题目】柯桥区某企业因为发展需要,从外地调运来一批94吨的原材料,现有甲、乙、丙三种车型共选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费6400元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?