题目内容
阅读下面一段:计算1+5+52+53…+599+5100
观察发现,上式从第二项起,每项都是它前面一项的5倍,如果将上式各项都乘以5,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
解:设S=1+5+52+53…+599+5100,①
则5S=5+52+…+5100+5101,②
②-①得4S=5101-1,则S=
| 5101-1 |
| 4 |
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于5),那么这列数的求和问题,均可用上述“错位相减”法来解决.
下面请你观察算式1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 22000 |
分析:由题中的例子知从第二项起,每项都是它前面一项的5倍,等式两边同乘以5,观察知算式1+
+
+
+…+
从第二项起,每项都是它前面一项的
倍,运用类比的方法,等式两边同时乘以
,再利用错位相减法即可求得结果.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2200 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:此式具备上述规律
设S=1+
+
+
+…+
,①
则
S=
+
+
+
+…+
,②
①-②得
S=1-
,
解得S=2-
.
故答案为:2-
.
设S=1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 22000 |
则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 22001 |
①-②得
| 1 |
| 2 |
| 1 |
| 22001 |
解得S=2-
| 1 |
| 22000 |
故答案为:2-
| 1 |
| 22000 |
点评:此题重在提高大家的模仿与应用能力,运用已知的信息解答新型问题,要充分理解题中信息,并灵活运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 27、阅读下面一段材料,回答问题.
27、阅读下面一段材料,回答问题.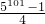 .
. +
+ +
+ +…+
+…+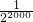 是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果. 的有理化因式是
的有理化因式是 ,
, 的有理化因式是
的有理化因式是 ,x
,x 的有理化因式是
的有理化因式是 。
。 =12-2=10;
=12-2=10; =150-18=132;
=150-18=132; =a2x-b2y。
=a2x-b2y。 +b
+b 乘a
乘a -b
-b ,其积是有理数,由此我们可以得出:
,其积是有理数,由此我们可以得出: -3
-3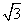 的有理化因式是_______;
的有理化因式是_______; +4
+4 的有理化因式是_______;
的有理化因式是_______;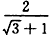 ;
; 。
。