题目内容
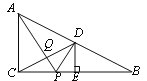
【题目】在△ABC中,AB=AC,BC=2,将△ABC绕点C顺针方向旋转α(0°<α<360°),得到△DEC,使点E在AB边上。
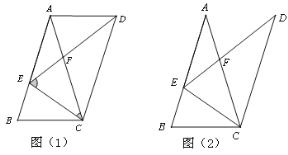
(1)如图1,连接AD,
①求证:四边形ABCD是平行四边形;
② 当AE=AD时,求旋转角α的度数;
(2)如图2,若AE=2BE,求AB的长。
【答案】(1)①详见解析;②旋转角α的度数为36°;(2)AB=2![]() .
.
【解析】
(1)①先根据旋转得:AB=CD,再由等腰三角形的性质和三角形内角和定理及外角的性质得:∠BAC=∠ACD,则AB∥CD,可得四边形ABCD是平行四边形;
②如图,在△ADE中,设∠3=x°,用x分别表示△ADE三个内角的度数,根据三角形的内角和列方程可得x的值,即可得旋转角α的度数;
(2)设BE=y,则AE=2y.AB=3y,证明△BCE∽△BAC,可得结论.
解:(1)①△ABC绕点C顺时针方向旋转得到△DEC
∴∠BCE=∠ACD BC=CE CD=CA
∴∠B=∠BEC
∵AB=AC ∴∠B=∠ACB ∴∠ACB=∠BEC
∴∠BCE=∠BAC
∵∠BCE=∠ACD
∴∠BAC=∠ACD
∴AB∥CD
∵CD=AC=AB
∴四边形ABCD是平行四边形 ;
②如图 ∵AE=AD ∴∠1=∠2
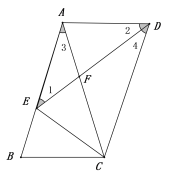
由旋转可得 ∠3=∠4
∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠DAC=∠ACB=∠B ∠1=∠4
在△ADE中,设∠3=x° 则∠4=x°,∠1=∠2=x°,∠B=90°-![]()
∵∠1+∠EAD+∠2=180°
∴x+(x+90-![]() )+x=180
)+x=180
∴x=36 ∴∠3=36°
∴旋转角α的度数为36° ;
(2)∵∠B=∠B,∠BCE=∠3
∴△BCE∽△BAC ∴![]()
设BE=y,则AE=2y,AB=3y
∴![]() 解得 y=
解得 y=![]()
∴AB=![]() .
.
故答案为:(1)①详见解析;②旋转角α的度数为36°;(2)AB=2![]() .
.

【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.