题目内容
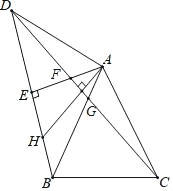
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(![]() ﹣1)EF.其中正确结论的个数为( )
﹣1)EF.其中正确结论的个数为( )
A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】
①根据△ABC为等边三角形,△ABD为等腰直角三角形的性质,以及顶角∠CAD=150°,即可判断,②求出![]() 与
与![]() 的度数即可判断. ③证明
的度数即可判断. ③证明
△ADF≌△BAH即可判断,④根据两组角对应相等的两个三角形相似即可判断.
⑤设![]() ,则
,则![]() 根据相似三角形的判定与性质即可得出结论.
根据相似三角形的判定与性质即可得出结论.
∵△ABC为等边三角形,△ABD为等腰直角三角形,
∴∠BAC=60°、![]()
∴![]() 是等腰三角形,且顶角∠CAD=150°,
是等腰三角形,且顶角∠CAD=150°,
∴∠ADC=15°,故①正确;
∵AE⊥BD,即∠AED=90°,
∴![]()
∴![]()
∴![]()
由![]() 知
知![]() 故②错误;
故②错误;
记AH与CD的交点为P,

由![]() 且∠AFG=60°知∠FAP=30°,
且∠AFG=60°知∠FAP=30°,
则![]()
在△ADF和△BAH中,
∵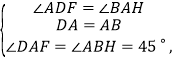
∴△ADF≌△BAH(ASA),
∴![]() ,故③正确;
,故③正确;
∵![]()
∴![]() ,故④正确;
,故④正确;
在![]() 中,设
中,设![]() ,则
,则![]()
设![]()
∵△ADF≌△BAH,
∴![]()
△ABE中,∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() 即
即![]()
整理,得: ![]()
由x≠0得![]() 即
即![]() 故⑤正确;
故⑤正确;
故选:B.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某市举行知识大赛,![]() 校、
校、![]() 校各派出
校各派出![]() 名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
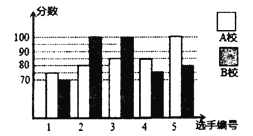
(1)根据图示填写下表:
平均数 | 中位数 | 众数 | |
|
| ||
|
| 80 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
【题目】为了迎接“炎帝故里寻根节”,某校开展了主题为“炎帝文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,整理调查数据制成了下面的表格和如图所示的不完整的扇形统计图.
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |

根据以上提供的信息,解答下列问题:
(1)本次问卷调查共抽取的学生人数为________,表中m的值为________;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生1 500人,请根据调查结果估计这些学生中“不太了解”炎帝文化知识的人数约为多少?