题目内容
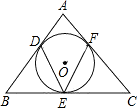 已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于
已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于
- A.96°
- B.48°
- C.24°
- D.72°
D
分析:连接OD、OF;根据切线的性质知:OD⊥AB,OF⊥AC,则四边形ADOF中,∠A+∠DOF=180°;那么解题的关键是求出∠DOF的度数,在⊙O中,∠DOF和∠DEF是同弧所对的圆心角和圆周角,根据圆周角定理,易求得∠DOF的度数,由此得解.
解答: 解:如图,连接OD、OE,则∠ODA=∠OFA=90°;
解:如图,连接OD、OE,则∠ODA=∠OFA=90°;
⊙O中,∠DOF=2∠DEF=2×54°=108°;
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=72°.
故选D.
点评:本题考查的是圆周角定理以及三角形内切圆的性质.
分析:连接OD、OF;根据切线的性质知:OD⊥AB,OF⊥AC,则四边形ADOF中,∠A+∠DOF=180°;那么解题的关键是求出∠DOF的度数,在⊙O中,∠DOF和∠DEF是同弧所对的圆心角和圆周角,根据圆周角定理,易求得∠DOF的度数,由此得解.
解答:
 解:如图,连接OD、OE,则∠ODA=∠OFA=90°;
解:如图,连接OD、OE,则∠ODA=∠OFA=90°;⊙O中,∠DOF=2∠DEF=2×54°=108°;
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=72°.
故选D.
点评:本题考查的是圆周角定理以及三角形内切圆的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( )
16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( )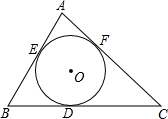 已知△ABC的内切圆半径r=
已知△ABC的内切圆半径r= 已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程.
已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程.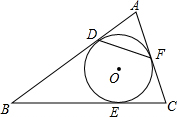 如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( )
如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( ) 上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.
上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.