题目内容
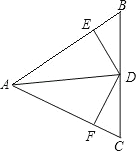
【题目】如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: .
【答案】①②③④.
【解析】
试题分析:在△ABC中,AB=AC,AD是△ABC的平分线,可知直线AD为△ABC的对称轴,再根据图形的对称性,逐一判断.
解:∵在△ABC中,AB=AC,AD是△ABC的平分线,
根据等腰三角形底边上的“三线合一”可知,AD垂直平分BC,①正确;
由①的结论,已知DE⊥AB,DF⊥AC,可证△ADE≌△ADF(AAS)
故有AE=AF,DE=DF,②正确;
AD是△ABC的平分线,根据角平分线性质可知,AD上的点到B、C两点距离相等,③正确;
根据图形的对称性可知,图中共有3对全等三角形,④正确.故填①②③④.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目