Question

【题目】如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD于F，交AC于E，若EG⊥BC于G，连结FG．说明四边形AFGE是菱形．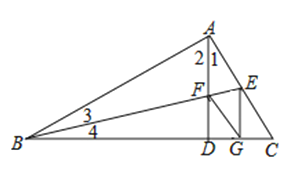

Answer 1

【答案】证明：∵在Rt△ABC中，∠BAC=90°，
∴BA⊥AE，
∵BE平分∠ABC，EG⊥BC，
∴∠3=∠4，AE=EG，
∵AD⊥BC，
∴AD∥EG，∠AFE=∠BFD=90°﹣∠4，
∵∠AEF=90°﹣∠3，
∴∠AEF=∠AFE，
∴AF=AE，
∴AF=EG，
∴四边形AFGE是平行四边形，
∴AFGE是菱形．
【解析】由在Rt△ABC中，∠BAC=90°，EG⊥BC，BE平分∠ABC，根据角平分线的性质，可得AE=EG，易求得△AEF是等腰三角形，即可得AF=AE=EG，继而证得四边形AFGE是平行四边形，则可得四边形AFGE是菱形．
【考点精析】根据题目的已知条件，利用菱形的判定方法的相关知识可以得到问题的答案，需要掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．