题目内容
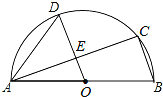
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
【答案】(1)∠CAD的度数为36°;(2)DE的长为4.
【解析】试题分析:(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
试题解析:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°-∠B=90°-70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=![]() =55°
=55°
∴∠CAD=∠DAO-∠CAB=55°-20°=35°;
(2)在直角△ABC中,BC=![]() .
.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=![]() BC=
BC=![]() .
.
又∵OD=![]() AB=6.5,
AB=6.5,
∴DE=OD-OE=6.5-![]() =4.
=4.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目