题目内容
已知两点O(0,0)、B(0,2),⊙A过点B且与x轴分别相交于点O、C,⊙A被y轴 分成段两圆弧,其弧长之比为3:1,直线l与⊙A切于点O,抛物线的顶点在直线l上运动.
分成段两圆弧,其弧长之比为3:1,直线l与⊙A切于点O,抛物线的顶点在直线l上运动.(1)求⊙A的半径;
(2)若抛物线经过O、C两点,求抛物线的解析式;
(3)过l上一点P的直线与⊙A交于C、E两点,且PC=CE,求点E的坐标;
(4)若抛物线与x轴分别相交于C、F两点,其顶点P的横坐标为m,求△PFC的面积关于m的函数解析式.
分析:(1)根据,⊙A被y轴分成段两圆弧,其弧长之比为3:1,可知弦OB所对的圆心角的度数为90°,即三角形OAB为等腰直角三角形,根据斜边OB长为2,因此圆A的半径应该是
;
(2)本题要分两种情况进行求解:
圆A的圆心在第一象限时,那么C点的坐标应是(2,0),
圆A的圆心在第二象限时,C点的坐标应该是(-2,0),
因此可设抛物线的解析式为y=ax(x-2)或y=ax(x+2).已知顶点坐标在直线l上,由于l与圆相切,在(1)已经得出∠BOA=45°,因此直线l与y轴的夹角为45°,那么直线l的解析式为y=x或y=-x.根据抛物线的对称性和O,C的坐标可知,抛物线的对称轴为x=1或x=-1,将横坐标代入直线l中即可求出顶点坐标,然后将其代入抛物线的解析式中即可得出所求的结果;
(3)本题可根据切割线定理求解,先根据直线l的解析式设出P点的坐标,如(m,-m)(m>0)那么OP=
m,根据切割线定理有OP2=PC•PE=2PC2=2m2,因此PC=m,由此可得出PC与P的纵坐标的绝对值相同,即PC⊥x轴,因此m=OC=2.即可得出P点的坐标;(另外一种情况,即当直线l的解析式为y=x时,解法同上)
(4)已知了P点的横坐标为m,即抛物线的对称轴为x=m,可据此求出FC的长,然后将m代入抛物线的解析式中求出P点的纵坐标,即可得出三角形的高,然后根据三角形的面积计算公式即可求得S,m的函数关系式.(本题要注意的线段的长不能为负数,因此要根据m的不同的取值范围进行分类讨论)
| 2 |
(2)本题要分两种情况进行求解:
圆A的圆心在第一象限时,那么C点的坐标应是(2,0),
圆A的圆心在第二象限时,C点的坐标应该是(-2,0),
因此可设抛物线的解析式为y=ax(x-2)或y=ax(x+2).已知顶点坐标在直线l上,由于l与圆相切,在(1)已经得出∠BOA=45°,因此直线l与y轴的夹角为45°,那么直线l的解析式为y=x或y=-x.根据抛物线的对称性和O,C的坐标可知,抛物线的对称轴为x=1或x=-1,将横坐标代入直线l中即可求出顶点坐标,然后将其代入抛物线的解析式中即可得出所求的结果;
(3)本题可根据切割线定理求解,先根据直线l的解析式设出P点的坐标,如(m,-m)(m>0)那么OP=
| 2 |
(4)已知了P点的横坐标为m,即抛物线的对称轴为x=m,可据此求出FC的长,然后将m代入抛物线的解析式中求出P点的纵坐标,即可得出三角形的高,然后根据三角形的面积计算公式即可求得S,m的函数关系式.(本题要注意的线段的长不能为负数,因此要根据m的不同的取值范围进行分类讨论)
解答: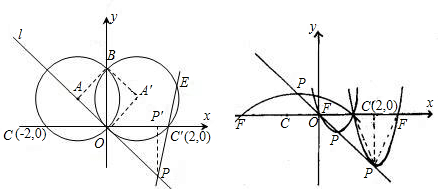 解:(1)
解:(1)
由弧长之比为3:1,
可得∠BAO=90°,(1分)
再由AB=AO=r,且OB=2,
得r=
;
(2)⊙A的切线l过原点,可设l为y=kx,
任取l上一点(b,kb),由l与y轴夹角为45°,
可得:b=-kb或b=kb,得k=-1或k=1,
∴直线l的解析式为y=-x或y=x
又由r=
,易得C(2,0)或C(-2,0)
由此可设抛物线解析式为y=ax(x-2)或y=ax(x+2)
再把顶点坐标代入l的解析式中得a=1
∴抛物线为y=x2-2x或y=x2+2x;
(3)当l的解析式为y=-x时,由P在l上,
可设P(m,-m)(m>0)
过P作PP′⊥x轴于P′,
∴OP′=|m|,PP′=|-m|,
∴OP=
=2m2,
又由切割线定理可得:OP2=PC•PE,且PC=CE,
得PC=C′E=m=PP′
∴C与P′为同一点,即PE⊥x轴于C,
∴m=-2,E(2,2)
同理,当l的解析式为y=x时,m=-2,E(-2,2);
(4)若C(2,0),此时l为y=-x,
∵P与点O、点C不重合,
∴m≠0且m≠2,
当m<0时,FC=2(2-m),高为|yp|即为-m,
∴S=
=m2-2m.
同理当0<m<2时,S=-m2+2m;当m>2时,S=m2-2m;
∴S=.
,
又若C(-2,0),
此时l为y=x,同理可得;S=.
.
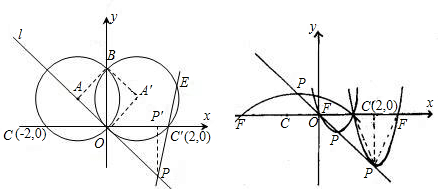 解:(1)
解:(1)由弧长之比为3:1,
可得∠BAO=90°,(1分)
再由AB=AO=r,且OB=2,
得r=
| 2 |
(2)⊙A的切线l过原点,可设l为y=kx,
任取l上一点(b,kb),由l与y轴夹角为45°,
可得:b=-kb或b=kb,得k=-1或k=1,
∴直线l的解析式为y=-x或y=x
又由r=
| 2 |
由此可设抛物线解析式为y=ax(x-2)或y=ax(x+2)
再把顶点坐标代入l的解析式中得a=1
∴抛物线为y=x2-2x或y=x2+2x;
(3)当l的解析式为y=-x时,由P在l上,
可设P(m,-m)(m>0)
过P作PP′⊥x轴于P′,
∴OP′=|m|,PP′=|-m|,
∴OP=
| m2+(-m)2 |
又由切割线定理可得:OP2=PC•PE,且PC=CE,
得PC=C′E=m=PP′
∴C与P′为同一点,即PE⊥x轴于C,
∴m=-2,E(2,2)
同理,当l的解析式为y=x时,m=-2,E(-2,2);
(4)若C(2,0),此时l为y=-x,
∵P与点O、点C不重合,
∴m≠0且m≠2,
当m<0时,FC=2(2-m),高为|yp|即为-m,
∴S=
| 2(2-m)•(-m) |
| 2 |
同理当0<m<2时,S=-m2+2m;当m>2时,S=m2-2m;
∴S=.
|
又若C(-2,0),
此时l为y=x,同理可得;S=.
|
点评:本题主要考查了切线的性质,等腰直角三角形的性质、二次函数解析式的确定,图形面积的求法等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
 已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标为( )
已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标为( ) 如图,在直角坐标系XOY中,已知两点O1(3,0)、B(-3,0),⊙O1与X轴交于原点0和点A,E是Y轴上的一个动点,设点E的坐标为(0,m).
如图,在直角坐标系XOY中,已知两点O1(3,0)、B(-3,0),⊙O1与X轴交于原点0和点A,E是Y轴上的一个动点,设点E的坐标为(0,m).