题目内容
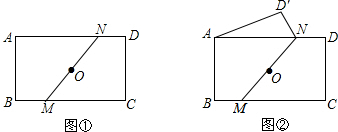
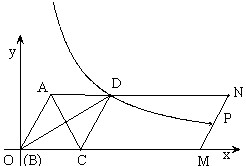
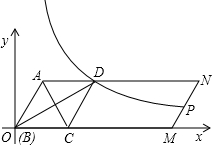
如图,?ABMN中,AC平分∠BAN交BM于C点,CD∥AB交AN于D点.
(1)判断四边形ABCD的形状并证明你的结论;
(2)以B点为坐标原点,BM所在的直线为横轴建立平面直角坐标系,若∠ABM=60°,A点横坐标为2,请直接写出A、C、D点坐标及经过D点的反比例函数解析式;
(3)设(2)中反比例函数的图象与MN交于P点,求当BM的长为多少时,P点为MN的中点.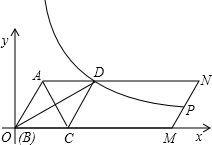
解:(1)是菱形,(1分)
证明:∵四边形ABMN是平行四边形
∴AD∥BC
∵CD∥AB
∴四边形ABCD是平行四边形(2分)
∵AC平分∠BAN
∴∠BAC=∠DAC
∵AD∥BC
∴∠CAD=∠ACB
∴∠BAC=∠ACB
∴BA=BC
∴?ABCD是菱形(4分)
(2)A(2,2 ),C(4,0),D(6,2
),C(4,0),D(6,2 ),
),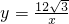 (8分)
(8分)
(3)设BM=a,
∵A(2,2 ),∠ABM=60°,
),∠ABM=60°,
∴点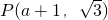 (10分)
(10分)
把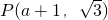 代入
代入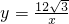 ,
,
解之得a=11.
所以当BM=11时,反比例函数的图象经过MN的中点.(12分)
分析:(1)首先证明四边形ABCD是平行四边形,然后证明其邻边BA和BC相等,即可证明四边形ABCD是菱形;
(2)利用平行四边形的性质可以得到三点的坐标分别为A(2,2 ),C(4,0),D(6,2
),C(4,0),D(6,2 );
);
(3)设BM=a,然后用a表示出点P的坐标为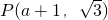 ,然后将点P的坐标代入所在反比例函数的解析式求得a的值即可.
,然后将点P的坐标代入所在反比例函数的解析式求得a的值即可.
点评:本题考查了反比例函数的知识,解题的关键是正确的利用平行四边形的性质及菱形的性质表示出点P的坐标.
证明:∵四边形ABMN是平行四边形
∴AD∥BC
∵CD∥AB
∴四边形ABCD是平行四边形(2分)
∵AC平分∠BAN
∴∠BAC=∠DAC
∵AD∥BC
∴∠CAD=∠ACB
∴∠BAC=∠ACB
∴BA=BC
∴?ABCD是菱形(4分)
(2)A(2,2
 ),C(4,0),D(6,2
),C(4,0),D(6,2 ),
),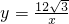 (8分)
(8分)(3)设BM=a,
∵A(2,2
 ),∠ABM=60°,
),∠ABM=60°,∴点
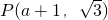 (10分)
(10分)把
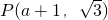 代入
代入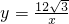 ,
,解之得a=11.
所以当BM=11时,反比例函数的图象经过MN的中点.(12分)
分析:(1)首先证明四边形ABCD是平行四边形,然后证明其邻边BA和BC相等,即可证明四边形ABCD是菱形;
(2)利用平行四边形的性质可以得到三点的坐标分别为A(2,2
 ),C(4,0),D(6,2
),C(4,0),D(6,2 );
);(3)设BM=a,然后用a表示出点P的坐标为
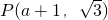 ,然后将点P的坐标代入所在反比例函数的解析式求得a的值即可.
,然后将点P的坐标代入所在反比例函数的解析式求得a的值即可.点评:本题考查了反比例函数的知识,解题的关键是正确的利用平行四边形的性质及菱形的性质表示出点P的坐标.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
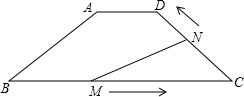 端点时,另一点也随之停止运动,设运动的时间为t秒.
端点时,另一点也随之停止运动,设运动的时间为t秒.