题目内容
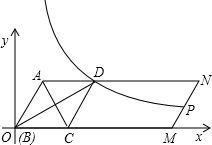
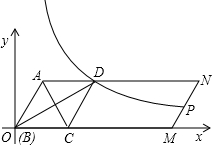
如图，□ABMN中，AC平分∠BAN交BM于C点，CD∥AB交AN于D点。
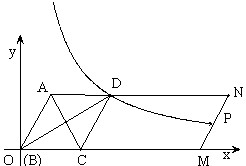
（1）判断四边形ABCD的形状并证明你的结论；
（2）以B点为坐标原点，BM所在的直线为横轴建立平面直角坐标系，若∠ABM=60°，A点横坐标为2，请直接写出A、C、D点坐标及经过D点的反比例函数解析式；
（3）设（2）中反比例函数的图象与MN交于P点，求当BM的长为多少时，P点为MN的中点。
（2）以B点为坐标原点，BM所在的直线为横轴建立平面直角坐标系，若∠ABM=60°，A点横坐标为2，请直接写出A、C、D点坐标及经过D点的反比例函数解析式；
（3）设（2）中反比例函数的图象与MN交于P点，求当BM的长为多少时，P点为MN的中点。
解：（1）是菱形，
证明：∵四边形ABMN是平行四边形
∴AD∥BC
∵CD∥AB
∴四边形ABCD是平行四边形
∵AC平分∠BAN
∴∠BAC=∠DAC
∵AD∥BC
∴∠CAD=∠ACB
∴∠BAC=∠ACB
∴BA=BC
∴□ABCD是菱形。
（2）A（2，2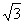
），C（4，0），D（6，2
），
。
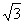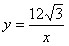（3）设BM=a，则点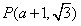
把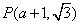
代入
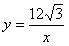
解得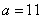
所以当BM=11时，反比例函数的图象经过MN的中点。
证明：∵四边形ABMN是平行四边形
∴AD∥BC
∵CD∥AB
∴四边形ABCD是平行四边形
∵AC平分∠BAN
∴∠BAC=∠DAC
∵AD∥BC
∴∠CAD=∠ACB
∴∠BAC=∠ACB
∴BA=BC
∴□ABCD是菱形。
（2）A（2，2
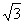），C（4，0），D（6，2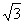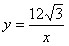），。（3）设BM=a，则点
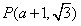
把
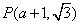代入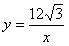解得
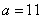
所以当BM=11时，反比例函数的图象经过MN的中点。
练习册系列答案
相关题目
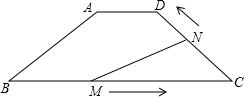端点时，另一点也随之停止运动，设运动的时间为t秒．
