题目内容
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若AB=6 cm,求△DEB的周长.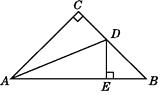
【答案】解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,∠C=∠DEA=90°.
在Rt△ACD和Rt△AED中, ![]()
∴Rt△ACD≌Rt△AED(HL)
.∴AC=AE.
∵CD=DE,
∴BC=CD+DB=DE+DB.
又∵AC=BC,
∴AE=AC=DE+DB,
∴DE+DB+BE=AB=6 cm.
∴△DEB的周长为6 cm.
【解析】根据角平分线上的点到角两边的距离相等及垂直的定义得出CD=DE,∠C=∠DEA=90°,然后利用HL判断出Rt△ACD≌Rt△AED,根据全等三角形对应边相等得出AC=AE.又CD=DE,从而得出BC=CD+DB=DE+DB.又AC=BC,从而得出AE=AC=DE+DB,根据三角形的周长得出DE+DB+BE=AB=6 cm。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目