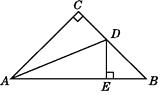
题目内容
【题目】如图,AE∥CF,AG,CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D.
求证:AB+CD=AC.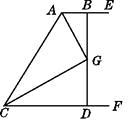
【答案】证明:过G作GH⊥AC于H,如图所示.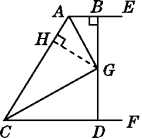
方法一:∵AE∥CF,BD⊥AE交CF于D,
∴GD⊥CF.
∵AG,CG分别平分∠EAC和∠FCA,
∴∠BAG=∠GAH,∠GCH=∠GCD.
易得∠BGA=∠HGA,∠HGC=∠DGC.
又由CD⊥GD,CH⊥GH,AH⊥GH,AB⊥GB.
易得CD=CH,AB=AH.
∴AB+CD=AH+CH=AC.
方法二:∵AE∥CF,BD⊥AE交CF于D.
∴GD⊥CF,
∵AG平分∠EAC,
∴BG=HG.
在Rt△AGH和Rt△AGB中,![]()
∴Rt△AGH≌Rt△AGB(HL).
∴AH=AB.
同理可得,CD=CH.
∴AB+CD=AH+CH=AC.
【解析】过G作GH⊥AC于H,方法一 :根据平行线的性质定理得出GD⊥CF.根据角平分线的定义∠BAG=∠GAH,∠GCH=∠GCD.根据等角的余角相等得出∠BGA=∠HGA,∠HGC=∠DGC.根据角平分线上的点到角两边的距离相等得出CD=CH,AB=AH,根据线段的和差及等量代换得出AB+CD=AH+CH=AC.
方法二:根据平行线的性质定理得出GD⊥CF,根据角平分线上的点到角两边的距离相等得出BG=HG,然后利用HL判断出Rt△AGH≌Rt△AGB,根据全等三角形对应边相等得出AH=AB.同理可得,CD=CH,根据线段的和差及等量代换得出AB+CD=AH+CH=AC.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目