题目内容
⊙O的半径OA＝1，弦AB、AC的长分别是、，则∠BAC的度数为 .
15°或75°．
试题分析：如图，分别作OD⊥AB，OE⊥AC，垂足分别是D、E．
∵OE⊥AC，OD⊥AB，根据垂径定理得AE=
AC=
，AD=AB=
.又∵OA＝1，∴
.根据特殊角的三角函数值可得∠AOE=60°，∠AOD=45°，
∴∠BAO=45°，∠CAO=90°
60°=30°.∴∠BAC=45°+30°=75°，或∠BAC′=45°
30°=15°．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
为线段PQ长度的最大值，
为线段PQ长度的最小值，图形M，N的平均距离
．
中，⊙O是以O为圆心，2的半径的圆，且A
，B
，求
及
；(直接写出答案即可)
与
轴交于点D，与
轴交于点F，记线段DF为图形G，求
；
，求圆心C的横坐标．
时，求∠DOE的度数.
,则点P与⊙O的位置关系是( )
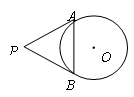
D．
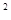，则扇形的半径是____．