题目内容
(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy(如图1),一次函数![]() 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数![]() 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数![]() 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
(本题满分12分,每小题满分各4分)
[解] (1) 根据两点之间距离公式,设M(a, ![]() a),由|MO |=| MA |, 解得:a=1,则M(1,
a),由|MO |=| MA |, 解得:a=1,则M(1, ![]() ),
),
即AM=![]() 。
。
(2) ∵ A(0, 3),∴ c=3,将点M代入y=x2+bx+3,解得:b= -![]() ,即:y=x2-
,即:y=x2-![]() x+3。
x+3。
(3) C(2, 2) (根据以AC、BD为对角线的菱形)。注意:A、B、C、D是按顺序的。
[解] 设B(0,m) (m<3),C(n,n2-![]() n+3),D(n,
n+3),D(n,![]() n+3),
n+3),
| AB |=3-m,| DC |=yD-yC=![]() n+3-(n2-
n+3-(n2-![]() n+3)=
n+3)=![]() n-n2,
n-n2,
| AD |=![]() =
=![]() n,
n,
| AB |=| DC |Þ3-m=![]() n-n2…j,|AB |=| AD |Þ3-m=
n-n2…j,|AB |=| AD |Þ3-m=![]() n…k。
n…k。
解j,k,得n1=0(舍去),或者n2=2,将n=2代入C(n,n2-![]() n+3),得C(2, 2)。
n+3),得C(2, 2)。
解析:略

练习册系列答案
相关题目
 沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线
沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线 与
与 轴交于A,B两点(点A在点B的右侧),且经过点C,(1)求直线
轴交于A,B两点(点A在点B的右侧),且经过点C,(1)求直线 及抛物线的解析式;(2)设抛物线的顶点为
及抛物线的解析式;(2)设抛物线的顶点为 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且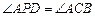 ,求点
,求点
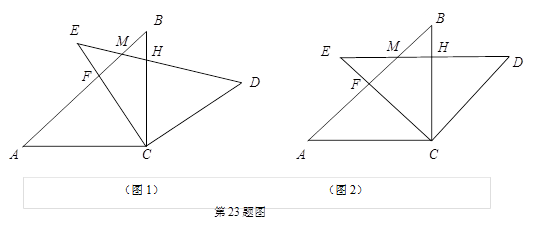
 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.



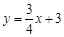 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.