��Ŀ����
����������12�֣�ÿС�����ָ�4�֣���֪ƽ��ֱ������ϵxOy����ͼ1����һ�κ���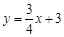 ��ͼ ����y�ύ�ڵ�A����M������������
��ͼ ����y�ύ�ڵ�A����M������������ ��ͼ���ϣ���MO��MA�����κ���y��x2��bx��c��ͼ����A��M��
��ͼ���ϣ���MO��MA�����κ���y��x2��bx��c��ͼ����A��M��
��1�����߶�AM�ij���
��2����������κ����Ľ���ʽ��
��3�������B��y���ϣ���λ�ڵ�A�·�����C���������κ�����ͼ���ϣ���D��һ�κ���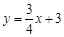 ��ͼ���ϣ����ı���ABCD�����Σ����C�����꣮
��ͼ���ϣ����ı���ABCD�����Σ����C�����꣮

(��������12�֣�ÿС�����ָ�4��)
[��] (1) ��������֮����빫ʽ����M(a,  a)����|
MO |=| MA |, ��ã�a=1����M(1,
a)����|
MO |=| MA |, ��ã�a=1����M(1,  ),
),
��AM= ��
��
(2) �� A(0, 3)���� c=3������M����y=x2+bx+3����ã�b= - ������y=x2-
������y=x2- x+3��
x+3��
(3) C(2, 2) (������AC��BDΪ�Խ��ߵ�����)��ע�⣺A��B��C��D�ǰ�˳��ġ�
[��] ��B(0,
m) (m<3)��C(n,
n2- n+3)��D(n,
n+3)��D(n,
 n+3)��
n+3)��
| AB |=3-m��| DC |=yD-yC= n+3-(n2-
n+3-(n2- n+3)=
n+3)= n-n2��
n-n2��
| AD |= =
=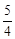 n��
n��
| AB |=| DC |Þ3-m= n-n2��j��|
AB |=| AD |Þ3-m=
n-n2��j��|
AB |=| AD |Þ3-m=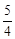 n��k��
n��k��
��j��k����n1=0(��ȥ)������n2=2����n=2����C(n,
n2- n+3)����C(2, 2)��
n+3)����C(2, 2)��
����������

 ��y������ƽ��3����λ���Ⱥ�ǡ�þ���B(-3��0)��y���ϵ�C�㣮��������
��y������ƽ��3����λ���Ⱥ�ǡ�þ���B(-3��0)��y���ϵ�C�㣮�������� ��
�� �ύ��A��B���㣨��A�ڵ�B���Ҳࣩ���Ҿ�����C����1����ֱ��
�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ���Ҿ�����C����1����ֱ�� �������ߵĽ���ʽ����2���������ߵĶ���Ϊ
�������ߵĽ���ʽ����2���������ߵĶ���Ϊ ����
���� �������ߵĶԳ����ϣ���
�������ߵĶԳ����ϣ��� �����
�����
 ��DE2��BE��CE����֤�ı���ABFC�Ǿ��Σ�
��DE2��BE��CE����֤�ı���ABFC�Ǿ��Σ�


