题目内容
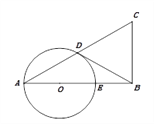
【题目】已知在△ABC中，∠ABC=90°，以AB上的一点O为圆心，以OA为半径的圆交AC于点D，交AB于点E．
（1）求证： 
；
（2）如果BD是⊙O的切线，D是切点，E是OB的中点，当BC=2时，求AC的长．
【答案】（1）证明见解析;(2)4.
【解析】试题分析：（1）本题利用两角法判定三角形相似，利用相似三角形的性质得出比例式即可；(2)利用切线的性质和特殊角的三角函数值判断出∠OBD=30°，进而得出∠BAC=30°，利用30°所对的直角边是斜边的一半即可得出.
试题解析：
（1）证明：连接DE,
∵AE是直径,∴∠ADE=90°.
∴∠ADE=∠ABC.
又∠A=∠A,∴△ADE∽△ABC. (3分)
∴
. (4分)
（2）解：连接OD,
∵BD是⊙O的切线,
∴OD⊥BD
∴∠ODB=90°. (5分)
∵在Rt△OBD中，E是OB的中点，
∴DE= 
=BE=OE=OD, (6分)
∴sin∠OBD=
.
∴∠OBD=30° (7分)
同理∠BAC=30°. (8分)
在Rt△ABC中,AC=2BC=2×2=4.(9分)
练习册系列答案
相关题目
【题目】某下岗职工购进一批货物，到集贸市场零售，已知卖出去的货物数量x与售价y的关系如下表：
数量x（千克） | 1 | 2 | 3 | 4 | 5 |
售价y（元） | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
写出用x表示y的公式是 ．
