题目内容
【题目】如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( ) 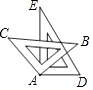
A.∠BAD≠∠EAC
B.∠DAC﹣∠BAE=45°
C.∠BAE+∠DAC=180°
D.∠DAC>∠BAE
【答案】C
【解析】解:∵是直角三角板,∴∠BAC=∠DAE=90°,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠BAD=∠EAC,①不成立;
∠DAC﹣∠BAE的值不固定,②不成立;
∵是直角三角板,
∴∠BAC=∠DAE=90°,
∴∠BAD+∠BAE+∠BAE+∠EAC=180°,
即∠BAE+∠DAC=180°,③成立;
∠DAC与∠BAE的大小不确定,
故选:C.
根据余角的定义、结合图形计算即可.

练习册系列答案
相关题目