题目内容
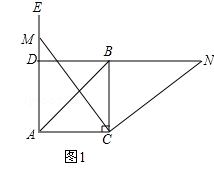
【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.
(1)如图1,求证:DF⊥DE; 
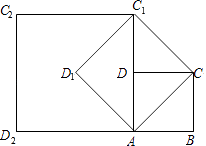
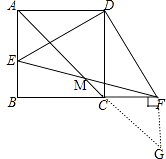
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点. 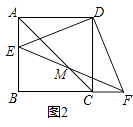
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠DCB=90°.
∴∠DCF=180°﹣90°=90°.
∴∠DAE=∠DCF.
在Rt△DAE和Rt△DCF中, ![]() ,
,
∴Rt△DAE≌Rt△DCF(HL).
∴∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴DF⊥DE.
(2)证明;过点F作GF⊥CF交AC的延长线于点G,
则∠GFC=90°.
∵正方形ABCD中,∠B=90°,
∴∠GFC=∠B.
∴AB∥GF.
∴∠BAC=∠G.
∵四边形ABCD是正方形,
∴AB=BC,
∴∠BAC=∠BCA=45°.
∴∠BAC=∠BCA=∠FCG=∠G=45°.
∴FC=FG.
∵△DAE≌△DCF,
∴AE=CF.
∴AE=FG.
在△AEM和△GFM中, 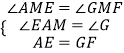 ,
,
∴△AEM≌△GFM(AAS).
∴ME=MF.
即M是EF的中点
【解析】(1)由正方形的性质得出DA=DC,∠DAE=∠DCB=90°.得出∠DAE=∠DCF.由HL证明Rt△DAE≌Rt△DCF,得出∠ADE=∠CDF,证出∠EDF=90°即可;(2)证明;过点F作GF⊥CF交AC的延长线于点G,则∠GFC=90°.AB∥GF.得出∠BAC=∠G.由正方形的性质证出FC=FG.得出AE=FG.由AAS证明△AEM≌△GFM,得出ME=MF即可.

练习册系列答案
相关题目