题目内容
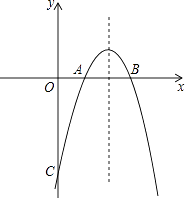
【题目】已知抛物线y=ax2+bx+c经过点A（0，3）、B（4，3）、C（1，0）、
（1）填空：抛物线的对称轴为直线x= ， 抛物线与x轴的另一个交点D的坐标为；
（2）求该抛物线的解析式．
【答案】
（1）2；（3，0）
（2）解：∵拋物线经过点C（1，0）、D（3，0），
∴设拋物线的解析式为y=a（x﹣1）（x﹣3）
由拋物线经过点A（0，3），得a=1
∴拋物线的解析式为y=x2﹣4x+3
【解析】解：（1）拋物线的对称轴为直线x=2；
拋物线与x轴的另一个交点D的坐标为（3，0）；
【考点精析】通过灵活运用二次函数的性质，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
【题目】纸箱厂用如图1所示的长方形和正方形纸板，做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒．
（1）现有正方形纸板172张，长方形纸板330张．若要做两种纸盒共l00个，设做竖式纸盒x个．
①根据题意，完成以下表格：
| 竖式纸盒(个) | 横式纸盒(个) |
x | ||
正方形纸板(张) | 2(100-x) | |
长方形纸板(张) | 4x |
②按两种纸盒的数量分，有哪几种生产方案?
（2）若有正方形纸板112张，长方形纸板
张，做成上述两种纸盒，纸板恰好用完．已知100<<110，则的值是 .
