题目内容
已知菱形ABCD周长为80cm,对角线AC:BD=3:4 那么菱形ABCD的面积=
384(cm)2
384(cm)2
.分析:根据菱形的性质,已知菱形的周长以及两条对角线长度的比例,利用勾股定理可求得对角线长,从而利用菱形的面积公式可以求得菱形ABCD的面积.
解答: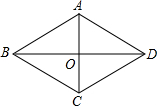 解:∵菱形ABCD的周长为80cm,
解:∵菱形ABCD的周长为80cm,
∴菱形的边长是80cm÷4=20cm;
又∵对角线AC:BD=3:4,
∴设菱形ABCD的对角线AC=3xcm,BD=4xcm(x>0),
则(
)2+(
)2=202,
∴
x2+4x2=400,即9x2+16x2=1600,
解得,x2=64;
∴S菱形=
AC•BD=
×3x•4x=6x2=6×64=384(cm)2;
故答案是:384(cm)2
 解:∵菱形ABCD的周长为80cm,
解:∵菱形ABCD的周长为80cm,∴菱形的边长是80cm÷4=20cm;
又∵对角线AC:BD=3:4,
∴设菱形ABCD的对角线AC=3xcm,BD=4xcm(x>0),
则(
| 3x |
| 2 |
| 4x |
| 2 |
∴
| 9 |
| 4 |
解得,x2=64;
∴S菱形=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:384(cm)2
点评:本题主要考查了菱形的性质.解答该题时,主要利用了菱形的四条边相等、两条对角线互相垂直的性质.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=24,且AE=6,则菱形的周长为( )
如图,已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=24,且AE=6,则菱形的周长为( )