题目内容
(本题满分10分)
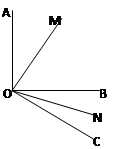
⑴如图,已知∠AOB=90º,∠BOC=30º,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;
⑵如果⑴中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
从⑴、⑵的结果中能得出什么结论?
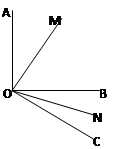
⑴如图,已知∠AOB=90º,∠BOC=30º,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;
⑵如果⑴中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
从⑴、⑵的结果中能得出什么结论?
(1)
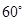 (2)
(2)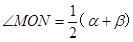
分析:
(1)根据∠MON的组成,利用角平分线的性质可得所求角的度数;
(2)根据(1)的计算方法可得所求结果;
结合(1)(2)可得求相邻2个角的角平分线的夹角的方法。
解答:
(1)∵OM平分∠AOB,ON平分∠BOC,∠AOB=90°,∠BOC=30°,
∴∠MOB=1/2∠AOB=45°,∠BON=1/2∠BOC=15°,
∴∠MON=∠MOB+∠BON=60°;
(2)由(1)得∠MON=∠MOB+∠BON=1/2∠AOB+1/2∠BON=1/2α+1/2β=1/2(α+β);
从⑴、⑵的结果看:有一个公共顶点,公共边,另一边分别在这条公共边的2侧的相邻2个角的角平分线组成的角等于这2个角组成的大角的一半。
点评:主要考查角平分线的性质的应用;运用类别的方法解决问题是解决本题的基本思路;从所求角的组成分析是解决本题的突破点。

练习册系列答案
相关题目
 ,能得到
,能得到 的是( )
的是( )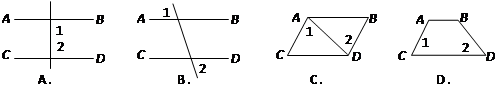

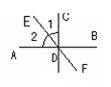
 被直线
被直线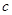 所截,若
所截,若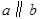 ,∠1=40°,则∠2的度数为 ( )
,∠1=40°,则∠2的度数为 ( )