题目内容
如图所示,直线AB、EF相交于点D,∠ADC="90" º ,若∠1与∠2的度数之比为1:4,则∠CDF、∠EDB的度数分别是 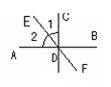

162°、108°
设∠1=x°,∠2=4x°,根据∠ADC=90°得出x+4x=90,求出x,即可求出∠1和∠2的度数,分别代入∠CDF=180°-∠1和∠EDB=180°-∠2求出即可.
解:设∠1=x°,∠2=4x°,
∵∠ADC=90°,
∴x+4x=90,
x=18,
即∠1=18°,∠2=4×18°=72°,
∵∠ADC=90°,
∴∠BDC=180°-90°=90°,
∵∠2=∠BDF=72°,
∴∠CDF=180°-∠1=162°,∠EDB=180°-∠2=108°,
故答案为:162°、108°.
本题考查了角的计算,主要考查学生的计算能力,注意:互为邻补角的两角的和是180°,即∠CDF=180°-∠1、∠EDB=180°-∠2.
解:设∠1=x°,∠2=4x°,
∵∠ADC=90°,
∴x+4x=90,
x=18,
即∠1=18°,∠2=4×18°=72°,
∵∠ADC=90°,
∴∠BDC=180°-90°=90°,
∵∠2=∠BDF=72°,
∴∠CDF=180°-∠1=162°,∠EDB=180°-∠2=108°,
故答案为:162°、108°.
本题考查了角的计算,主要考查学生的计算能力,注意:互为邻补角的两角的和是180°,即∠CDF=180°-∠1、∠EDB=180°-∠2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
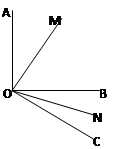
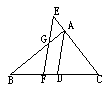
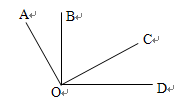
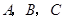 在同一直线上,若
在同一直线上,若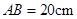 ,
,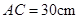 ,则
,则 的长是( )
的长是( )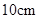
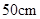
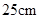
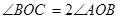 ,
, 平分
平分 ,∠BOD=180,求
,∠BOD=180,求