题目内容
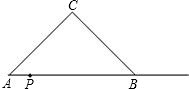
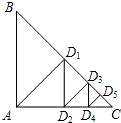如图，等腰Rt△ABC的直角边长为32，从直角顶点A作斜边BC的垂线交BC于D1，再从D1作D1D2⊥AC交AC于D2，再从D2作D2D3⊥BC交BC于D3，…，则AD1+D2D3+D4D5+D6D7+D8D9=________；D1D2+D3D4+D5D6+D7D8+D9D10=________．
31
31
分析：根据三角形的中位线定理，找出D4D5是D2D3的中位线，D2D3是AD1的中位线，D3D4是D1D2的中位线，以此类推，可以计算结果．
解答：根据中位线定理，中位线为对应边的长度的一半，我们可知：
（1）
=
，
所以AD1+D2D3+D4D5+D6D7+D8D9=AD1（1+
+
+
+
）=
，
因为△ABC为等腰直角三角形，且AD1⊥BC，
所以D1为BC的中点，且
=
，
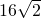所以AD1+D2D3+D4D5+D6D7+D8D9=
；
（2）D1D2+D3D4+D5D6+D7D8+D9D10=D1D2（1++++）=
，
D1为BC的中点，D2为AC的中点，所以D1D2=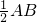
=16，
所以D1D2+D3D4+D5D6+D7D8+D9D10=
．
因此第一个空填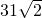
；第二个空填31．
故答案为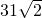；31．
点评：此题关键是考查中位线定理在三角形中的应用，找出中位线为对应边长的一半的规律，解决问题．
31分析：根据三角形的中位线定理，找出D4D5是D2D3的中位线，D2D3是AD1的中位线，D3D4是D1D2的中位线，以此类推，可以计算结果．
解答：根据中位线定理，中位线为对应边的长度的一半，我们可知：
（1）
=，所以AD1+D2D3+D4D5+D6D7+D8D9=AD1（1+
+++）=，因为△ABC为等腰直角三角形，且AD1⊥BC，
所以D1为BC的中点，且
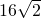=，所以AD1+D2D3+D4D5+D6D7+D8D9=
；（2）D1D2+D3D4+D5D6+D7D8+D9D10=D1D2（1+
+++）=，D1为BC的中点，D2为AC的中点，所以D1D2=
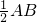=16，所以D1D2+D3D4+D5D6+D7D8+D9D10=
．因此第一个空填
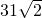；第二个空填31．故答案为
；31．点评：此题关键是考查中位线定理在三角形中的应用，找出中位线为对应边长的一半的规律，解决问题．
练习册系列答案
相关题目
PQ=AP，以PQ为一边向上作正方形PQMN，设正方形PQMN与Rt△ABC重叠部分的面积为S．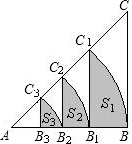
如图，等腰Rt△ABC的直角边长为4，以A为圆心，直角边AB为半径作弧BC1，交斜边AC于点C1，C1B1⊥AB于点B1，设弧BC1，C1B1，B1B围成的阴影部分的面积为S1，然后以A为圆心，AB1为半径作弧B1C2，交斜边AC于点C2，C2B2⊥AB于点B2，设弧B1C2，C2B2，B2B1围成的阴影部分的面积为S2，按此规律继续作下去，得到的阴影部分的面积S3=
如图，等腰Rt△ABC中斜边AB=4，O是AB的中点，以O为圆心的半圆分别与两腰相切于点D、E，图中阴影部分的面积是多少？请你把它求出来．（结果用π表示）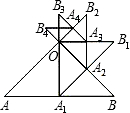
已知：如图，等腰Rt△OAB的直角边OA的长为1，以AB边上的高OA1为直角边，按逆时针方向作等腰Rt△OA1B1，A1B1与OB相交于点A2．若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2，A2B2与OB1相交于点A3，按此作法进行下去，得到△OA3B3，△OA4B4，…，则△OA6B6的周长是
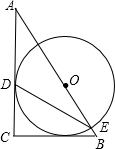如图，等腰Rt△ABC，AC=BC，以斜边AB中点O为圆心作⊙O与AC边相切于点D，交AB于点E，连接DE．