题目内容
如图,等腰Rt△ABC中,CA=CB=8| 2 |
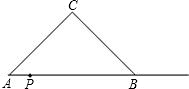 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.(1)求S与x的函数关系式,并写出自变量x的取值范围;
(2)S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
分析:(1)此题要分情况讨论:当0<x≤
时,重叠部分的面积即为正方形的面积;当
<x<8时,则重叠部分的面积即为正方形的面积减去等腰直角三角形的面积;当8≤x<16时,重叠部分的面积即为等腰直角三角形的面积;
(2)分别求得每一种情况的面积最大值,再进一步比较,取其中的面积最大值即可.
| 16 |
| 3 |
| 16 |
| 3 |
(2)分别求得每一种情况的面积最大值,再进一步比较,取其中的面积最大值即可.
解答: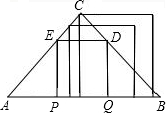 解:(1)如图,当0<x≤
解:(1)如图,当0<x≤
时,则S=x2;
当
<x<8时,则S=x2-
(x-16+2x)2=-
x2+48x-128;
当8≤x<16时,则S=
(16-x)2=
x2-16x+128.
(2)当0<x≤
时,则S=x2,则当x=
时,最大值S=
;
当
<x<8时,则S=x2-
(x-16+2x)2=-
x2+48x-128,则当x=
时,最大值S=
;
当8≤x<16时,则S=
(16-x)2=
x2-16x+128,当x=8时,最大值S=32.
综上所述,当x=
时,最大值S=
.
 解:(1)如图,当0<x≤
解:(1)如图,当0<x≤| 16 |
| 3 |
当
| 16 |
| 3 |
| 1 |
| 2 |
| 7 |
| 2 |
当8≤x<16时,则S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当0<x≤
| 16 |
| 3 |
| 16 |
| 3 |
| 256 |
| 9 |
当
| 16 |
| 3 |
| 1 |
| 2 |
| 7 |
| 2 |
| 48 |
| 7 |
| 256 |
| 7 |
当8≤x<16时,则S=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,当x=
| 48 |
| 7 |
| 256 |
| 7 |
点评:此题关键是能够正确分析出重叠的不同情况,能够根据建立的二次函数关系式,分析得到其最大值.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
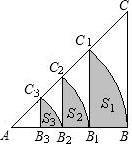 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=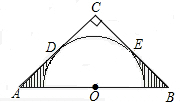 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)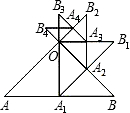 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是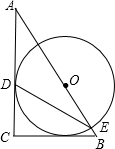 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.