题目内容
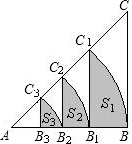 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=分析:每一个阴影部分的面积都等于扇形的面积减去等腰直角三角形的面积.
此题的关键是求得AB2、AB3的长.根据等腰直角三角形的性质即可求解.
此题的关键是求得AB2、AB3的长.根据等腰直角三角形的性质即可求解.
解答:解:根据题意,得
AC1=AB=4.
所以AC2=AB1=2
.
所以AC3=AB2=2.
所以AB3=
.
所以阴影部分的面积S3=
-
×2=
-1.
AC1=AB=4.
所以AC2=AB1=2
| 2 |
所以AC3=AB2=2.
所以AB3=
| 2 |
所以阴影部分的面积S3=
| 45π×4 |
| 360 |
| 1 |
| 2 |
| π |
| 2 |
点评:此题综合运用了等腰直角三角形的性质和扇形的面积公式.

练习册系列答案
相关题目
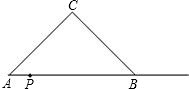 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S. 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)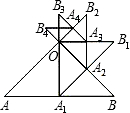 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是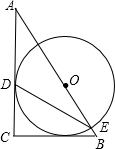 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.