题目内容
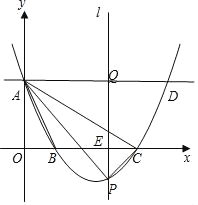
【题目】如图，A、B、C、D是矩形的四个顶点，AB=16cm，BC=6cm，动点P从点A出发，以3cm/s的速度向点B运动，直到点B为止；动点Q同时从点C出发，以2cm/s的速度向点D运动，当时间为_______时，点P和点Q之间的距离是10cm
【答案】
或
【解析】
求出当PQ∥BC即BP=CQ时的时间，从而确定t的范围并进行分类讨论，分两类：①当0≤t≤3.2；②当3.2＜t≤8，表示出对应线段的长度，结合勾股定理分别列出方程，解方程并对t进行取舍即可.
设时间为t，
当PQ∥BC时，BP=CQ，
16﹣3t=2t，解得t=3.2s，
点P从A点运动至B点的时间为：16÷3=
s，
点Q从C点运动至D点的时间为：16÷2=8s，
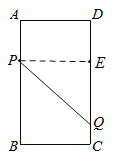
①当0≤t≤3.2时，如图，作PE⊥CD交CD于点E，
由题意得AP=DE=3t，CQ=2t，PE=6，
∴EQ=16﹣5t，
∵PE2+EQ2=PQ2，
∴62+（16﹣5t）2=102，
解得t1=，t2=（舍去）；
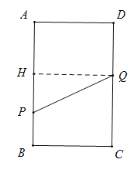
②当3.2＜t≤8时，如图作QH⊥AB交AB于点H，
由题意得AP=3t，CQ=2t， DH=6，
∴AH=DQ=16﹣2t，
∴PH=5t﹣16，
∵PH2+HQ2=PQ2，
∴(5t﹣16)2+62=102，
解得t1=（舍去），t2=；
∴t=或.
故答案为或.
【题目】由于雾霾天气持续笼罩某地区，口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩，销售完后共获利2800元，其进价和售价如下表：
甲种口罩 | 乙种口罩 | |
进价（元/袋） | 20 | 25 |
售价（元/袋） | 26 | 35 |
（1）求该商店购进甲、乙两种口罩各多少袋？
（2）该商店第二次仍以原价购进甲、乙两种口罩，购进乙种口罩袋数不变，而购进甲种口罩袋数是第一次的2倍，甲种口罩按原售价出售，而乙种口罩让利销售.若两种口罩销售完毕，要使第二次销售活动获利不少于3680元，则乙种口罩最低售价为每袋多少元？
