题目内容
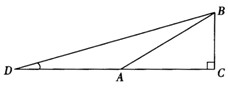
已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB= .
.(1)求DC的长;
(2)求AD的长;
(3)求AB的长.
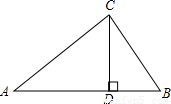
【答案】分析:(1)在Rt△DCB中,已知BC,DB根据勾股定理可以求DC;
(2)在Rt△ADC中,已知AC,DC根据勾股定理可以求AD;
(3)已知AD,DB,根据AB=AD+DB可以求AB.
解答:解:(1)在Rt△DCB中,DC2+DB2=BC2,
∴DC2=9- ,
,
∴DC= ;
;
(2)在Rt△ACD中,AD2+CD2=AC2,
∴AD2=16- ,
,
∴AD= ;
;
(3)AB=AD+DB= +
+ =5.
=5.
点评:本题考查了勾股定理在直角三角形中的灵活运用,本题中正确的选择直角三角形运用勾股定理是解题的关键.
(2)在Rt△ADC中,已知AC,DC根据勾股定理可以求AD;
(3)已知AD,DB,根据AB=AD+DB可以求AB.
解答:解:(1)在Rt△DCB中,DC2+DB2=BC2,
∴DC2=9-
 ,
,∴DC=
 ;
;(2)在Rt△ACD中,AD2+CD2=AC2,
∴AD2=16-
 ,
,∴AD=
 ;
;(3)AB=AD+DB=
 +
+ =5.
=5.点评:本题考查了勾股定理在直角三角形中的灵活运用,本题中正确的选择直角三角形运用勾股定理是解题的关键.

练习册系列答案
相关题目
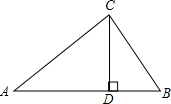 已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=
已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=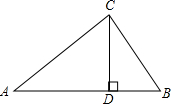 已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=
已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=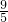 .
.
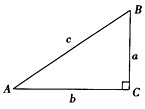
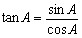 。
。