��Ŀ����
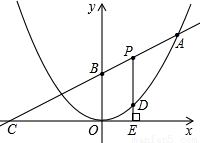
��ͼ��֪���κ���ͼ��Ķ���Ϊԭ�㣬ֱ��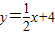 ��ͼ����ö��κ�����ͼ����A�㣨8��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
��ͼ����ö��κ�����ͼ����A�㣨8��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB����1����������κ����Ľ���ʽ��B�����ꣻ
��2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ����D�㣬��x�ύ�ڵ�E�����߶�PD�ij�Ϊh����P�ĺ�����Ϊt����h��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£����߶�AB���Ƿ���ڵ�P��ʹ���Ե�P��D��BΪ��������������BOC���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
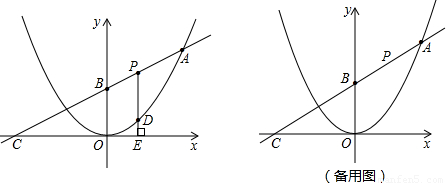
���𰸡���������1��������κ����Ľ���ʽΪy=ax2����A�㣨8��8������y=ax2�������������κ����Ľ���ʽ������ֱ�� ��y��Ľ��������Ϊ0�������B������Ϊ��
��y��Ľ��������Ϊ0�������B������Ϊ��
��2����P���� ���Һ�����Ϊt���ó�P�������Ϊ��t��
���Һ�����Ϊt���ó�P�������Ϊ��t�� t+4��������PD��x����E����t��ʾ��D��E�����꣬�ٸ���PD=h�����h=-
t+4��������PD��x����E����t��ʾ��D��E�����꣬�ٸ���PD=h�����h=- x2+
x2+ t+4��������P��AB���غ�����AB�ϣ��ó�t��ȡֵ��Χ��
t+4��������P��AB���غ�����AB�ϣ��ó�t��ȡֵ��Χ��
��3���ȹ���B��BF��PD��F���ó�PF= t+4-4=
t+4-4= t��BF=t���ٸ��ݹ��ɶ����ó�PB��BC��ֵ���ټ����PBO�ס�BOC���ó�
t��BF=t���ٸ��ݹ��ɶ����ó�PB��BC��ֵ���ټ����PBO�ס�BOC���ó� =
= ���������t1��t2��ֵ���Ӷ����P������ꣻ
���������t1��t2��ֵ���Ӷ����P������ꣻ
����⣺��1����˶��κ����Ľ���ʽΪy=ax2��
��A�㣨8��8���ڶ��κ���y=ax2�ϣ�
��8=a×82��
��a= ��
��
��y= x2��
x2��
��ֱ�� ��y��Ľ���ΪB��
��y��Ľ���ΪB��
��B����������0��4����
��2��P���� ���Һ�����Ϊt��
���Һ�����Ϊt��
��P��t�� t+4����
t+4����
��PD��x����E��
��D��t�� t2����E��t��0����
t2����E��t��0����
��PD=h��
�� t+4-
t+4- x2=h��
x2=h��
��h=- x2+
x2+ t+4��
t+4��
��P��AB���غ�����AB�ϣ�
��0��t��8��
��3�����ڣ�
��1����BD��PEʱ��
��PBD�ס�BCO��
�� =
= ��
��
�� =
= ��
��
��h= t��
t��
��- x2+
x2+ t+4=
t+4= t��
t��
x=4 ��x=-4
��x=-4 ����ȥ��
����ȥ��
��P����������ǣ� ×4
×4 +4=2
+4=2 +4��
+4��
���ʱP��������ǣ���4 ��2
��2 +4��
+4��
��2����DB��PCʱ��
��PBD�ס�BCO��
����B��BF��PD��
��F��t��4����
��PF= t+4-4=
t+4-4= t��
t��
BF=t��
���ݹ��ɶ����ã�
PB= =
= t��
t��
BC= =
= =4
=4
�����PBO�ס�BOC��
���� =
= ��
��
�� =
= ��
��
��ã�t1=-8+4 ��t2=-8-4
��t2=-8-4 ������������ȥ����
������������ȥ����
�� t+4=
t+4= ��-8+4
��-8+4 ��+4=2
��+4=2 ��
��
��P��-8+4 ��2
��2 ����
����
���������⿼���˶��κ������ۺϣ��ڽ���ʱҪ�������ö��κ�����ͼ�������������κ����Ľ���ʽ���������ν��˼������DZ���Ĺؼ���
 ��y��Ľ��������Ϊ0�������B������Ϊ��
��y��Ľ��������Ϊ0�������B������Ϊ����2����P����
 ���Һ�����Ϊt���ó�P�������Ϊ��t��
���Һ�����Ϊt���ó�P�������Ϊ��t�� t+4��������PD��x����E����t��ʾ��D��E�����꣬�ٸ���PD=h�����h=-
t+4��������PD��x����E����t��ʾ��D��E�����꣬�ٸ���PD=h�����h=- x2+
x2+ t+4��������P��AB���غ�����AB�ϣ��ó�t��ȡֵ��Χ��
t+4��������P��AB���غ�����AB�ϣ��ó�t��ȡֵ��Χ����3���ȹ���B��BF��PD��F���ó�PF=
 t+4-4=
t+4-4= t��BF=t���ٸ��ݹ��ɶ����ó�PB��BC��ֵ���ټ����PBO�ס�BOC���ó�
t��BF=t���ٸ��ݹ��ɶ����ó�PB��BC��ֵ���ټ����PBO�ס�BOC���ó� =
= ���������t1��t2��ֵ���Ӷ����P������ꣻ
���������t1��t2��ֵ���Ӷ����P������ꣻ����⣺��1����˶��κ����Ľ���ʽΪy=ax2��
��A�㣨8��8���ڶ��κ���y=ax2�ϣ�
��8=a×82��
��a=
 ��
����y=
 x2��
x2����ֱ��
 ��y��Ľ���ΪB��
��y��Ľ���ΪB����B������Ϊ����0��4����
��2��P����
 ���Һ�����Ϊt��
���Һ�����Ϊt����P��t��
 t+4����
t+4������PD��x����E��
��D��t��
 t2����E��t��0����
t2����E��t��0������PD=h��
��
 t+4-
t+4- x2=h��
x2=h����h=-
 x2+
x2+ t+4��
t+4��
��P��AB���غ�����AB�ϣ�
��0��t��8��
��3�����ڣ�
��1����BD��PEʱ��
��PBD�ס�BCO��
��
 =
= ��
����
 =
= ��
����h=
 t��
t����-
 x2+
x2+ t+4=
t+4= t��
t��x=4
 ��x=-4
��x=-4 ����ȥ��
����ȥ����P����������ǣ�
 ×4
×4 +4=2
+4=2 +4��
+4�����ʱP��������ǣ���4
 ��2
��2 +4��
+4����2����DB��PCʱ��
��PBD�ס�BCO��
����B��BF��PD��

��F��t��4����
��PF=
 t+4-4=
t+4-4= t��
t��BF=t��
���ݹ��ɶ����ã�
PB=
 =
= t��
t��BC=
 =
= =4
=4
�����PBO�ס�BOC��
����
 =
= ��
����
 =
= ��
����ã�t1=-8+4
 ��t2=-8-4
��t2=-8-4 ������������ȥ����
������������ȥ������
 t+4=
t+4= ��-8+4
��-8+4 ��+4=2
��+4=2 ��
����P��-8+4
 ��2
��2 ����
�������������⿼���˶��κ������ۺϣ��ڽ���ʱҪ�������ö��κ�����ͼ�������������κ����Ľ���ʽ���������ν��˼������DZ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
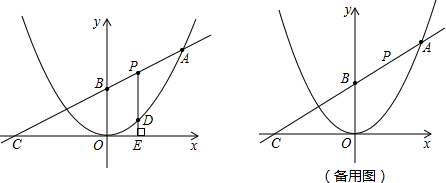


 ��ͼ����ö��κ�����ͼ����A��(8��8)��ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
��ͼ����ö��κ�����ͼ����A��(8��8)��ֱ����x��Ľ���ΪC����y��Ľ���ΪB��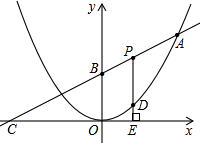
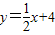 ��ͼ����ö��κ�����ͼ����A�㣨8��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
��ͼ����ö��κ�����ͼ����A�㣨8��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
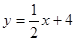 ��ͼ����ö��κ�����ͼ����A��(8��8)��ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
��ͼ����ö��κ�����ͼ����A��(8��8)��ֱ����x��Ľ���ΪC����y��Ľ���ΪB��