题目内容
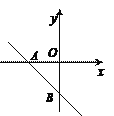
【题目】直线y＝－x－2交x轴于点A，交y轴于点B，一抛物线的顶点为A，且经过点B．
（1）求该抛物线的解析式；
（2）若点C（m，－4.5）在抛物线上，求m的值
【答案】（1）y=-0.5(x+2) 
；(2)1或-5
【解析】试题分析：（1）利用x轴上的点y坐标为0，y轴上的点x坐标为0代入直线的表达式求出A、B点的坐标，再利用顶点坐标式待定系数法求出抛物线的表达式；
（2）把x=m时，y=﹣4.5代入抛物线的表达式求出m．
试题解析：解：（1）由直线y=﹣x﹣2，令x=0，则y=﹣2，∴点B坐标为（0，﹣2），令y=0，则x=﹣2，∴点A坐标为（﹣2，0），设抛物线解析式为y=a（x﹣h）2+k．∵抛物线顶点为A，且经过点B，∴y=a（x+2）2，∴﹣2=4a，解得：a=﹣0.5，∴抛物线解析式为y=﹣0.5（x+2）2，即y=﹣0.5x2﹣2x﹣2；
（2）∵点C（m，﹣4.5）在抛物线y=﹣0.5x2﹣2x﹣2上，∴﹣0.5m2﹣2m﹣2=﹣4.5，∴m2+4m﹣5=0，解得：m1=1，m2=﹣5．
练习册系列答案
相关题目
【题目】某市居民使用自来水按如下标准收费（水费按月缴纳）：
户月用水量 | 单价 |
不超过12 m3的部分 | a元∕m3 |
超过12 m3但不超过20 m3的部分 | 1.5a元∕m3 |
超过20 m3的部分 | 2a元∕m3 |
(1) 当a＝2时，某用户一个月用了28 m3水，求该用户这个月应缴纳的水费；
(2) 设某户月用水量为n 立方米，当n＞20时，则该用户应缴纳的水费_____________元（用含a、n的整式表示）；
(3) 当a＝2时，甲、乙两用户一个月共用水40 m3，已知甲用户缴纳的水费超过了24元，设甲用户这个月用水xm3，，试求甲、乙两用户一个月共缴纳的水费（用含x的整式表示）．
