题目内容
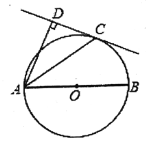
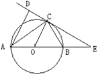
【题目】如图,AB是⊙0的直径,AB=10,CD是⊙0的切线,C为切点,交直线AB于E,AD⊥CD于D,AD=2CD.
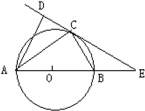
(1)求证:∠CAB=∠CAD;
(2)求CD的长;
(3)求AE的长.
【答案】(1)证明过程见解析;(2)4;(3)![]() .
.
【解析】
(1)根据切线和垂直得出∠OCA=∠DAC,再根据OA=OC得出∠OCA=∠OAC,即可得出答案;
(2)先求出△ACB∽△ADC得出AC=2CB,再结合勾股定理求出CB和AC的值,进而在△ACD中利用勾股定理求出CD和AD的值,即可得出答案;
(3)根据已知证出△ADE∽△OCE,再根据相似三角形对应边成比例即可得出答案.
(1)连接OC
∵CD是圆O的切线
∴∠OCD=∠OCE=90°
∴∠OCA+∠ACD=90°
又AD⊥CD
∴∠DAC+∠DCA=90°
∴∠OCA=∠DAC
又∵OC=OA
∴∠OCA=∠OAC
∴∠BAC=∠DAC
(2)∵AB是圆O的直径
∴∠ACB=90°
∴△ACB∽△ADC
又AD=2CD
∴AC=2CB
设AC=2x,CB=x
![]()
解得:![]() (负值舍去)
(负值舍去)
设CD=y,则AD=2y
则![]()
解得:y=±4(负值舍去)
∴CD=4
(3)∵CD=4,AD=8
∵AB是圆O的直径,AB=10
∴OA=OB=5
∴OE=AE-OA=AE-5
∵∠ADE=∠OCE,∠E=∠E
∴△ADE∽△OCE
∴![]()
即![]()
解得:AE=![]()

练习册系列答案
相关题目