题目内容
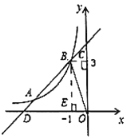
【题目】如图①，抛物线y＝﹣
x2+x+4与x轴交于A，B两点，与y轴交于点C，点D为线段AC的中点，直线BD与抛物线交于另一点E，与y轴交于点F．
（1）求直线BD的解析式；
（2）如图②，点P是直线BE上方抛物线上一动点，连接PD，PF，当△PDF的面积最大时，在线段BE上找一点G，使得PG﹣
GE的值最小，求出点G的坐标及PG﹣GE的最小值；
（3）将抛物线沿直线AC平移，点A，C平移后的对应点为A′，C'．在平面内有一动点H，当以点B，A'，C'，H为顶点的四边形为平行四边形时，在直线AC上方找一个满足条件的点H，与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时，求出点A′的坐标．
【答案】（1）y＝
x+1；（2）点G（，
），最小值为
；（3）（3，1）、（
+1，3﹣）、（1﹣，3+）、（5+，﹣﹣1）、（5﹣，﹣1）．
【解析】
（1）令-x2+x+4=0，可求出点A和点B的坐标，令x=0，可求出点C的坐标，再根据点D时AC的中点，可求出点D的坐标，利用待定系数法求直线解析式即可．（2）求三角形的面积最值可以转化为求线段长度的最大值，利用点坐标表示线段长度，配方求最值，求PG-
GE的最小值，可将不共线的线段转换为共线的线段长度．（3）理解题意利用轴对称图形就是找等腰三角形，再分情况讨论即可．
解：（1）令﹣x2+x+4＝0，解得x1＝﹣2，x2＝4，
∴B（﹣2，0），A（4，0），
令x＝0，y＝4，
∴C（0，4），
∵D为AC的中点，
∴D（2，2），
设直线BD的解析式为y＝kx+b（k≠0），代入点B和点D，
，
解得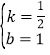
，
∴直线BD的解析式为y＝x+1．
（2）如图所示
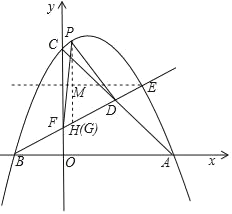
过点P作y轴的平行线，交BE交于点H，
设点P的坐标为（t，﹣t2+t+4），
则点H为（t， t+1），
∴PH＝﹣t2+t+4﹣（t+1）＝﹣（t﹣）2+
，
当t＝时，PH最大，此时点P为（，
），
当PH最大时，△PDF的面积也最大．
∵直线BD的解析式为y＝x+1，
令x＝0，y＝1，∴点F（0，1），
在Rt△BFO中，根据勾股定理，BF＝
，
∴sin∠FBO＝
过点E作x轴的平行线与过点G作y轴的平行线交于点M，
∴∠MEG＝∠FBO，
∴MG＝EGsin∠MEG＝EG，
∴PG﹣GE＝PG﹣MG，
当P、M、G三点共线时，PG﹣MG＝PM，否则都大于PM，
∴当P、M、G三点共线时，PG﹣MG最小，此时点G与点H重合，
令﹣x2+x+4＝x+1，
解得x1＝3，x2＝﹣2，
∴点E（3，
），
∴PM＝﹣＝，
∴点G（，），
∴点G（，），PG﹣GE的最小值为．
（3）如图所示，
当以点B，A'，C'，H为顶点的四边形为平行四边形时，
在直线AC下方的点H只有两个，点H1和点H2，
过点B作AC的平行线交y轴于点G，∴G（0，﹣2）
∵点A（4，0），点C（0，4），
∴AC＝4
，
∴BH1＝BH2＝4，
∵∠CAO＝45°，
∴H1（﹣6，4），H2（2，﹣4），
在y轴上截取点E，使EC＝CG，则点E（0，10），
过点E作AC的平行线，则在直线AC上方的点H一定在这条平行线上，
当△H1H2H3为等腰三角形时即为轴对称图形，
①当H1H3＝H2H3时，
直线EH3的解析式为y＝﹣x+10，
设H3（m，﹣m+10），
H1H3＝
，
H2H3＝
，
解得m＝4，∴H3（4，6），
∴A′（3，1）．
②当H1H3＝H1H2时，
∵H1H3＝，H1H2＝8，
解得m1＝2，m2＝﹣2，此时点H3（2，10﹣2）或（﹣2，10+2），
∴A′（+1，3﹣）或（1﹣，3+）．
③当H2H3＝H1H2时，
∵H2H3＝
，H1H2＝8，
解得m1＝8+2，m2＝8﹣2，此时点H3（8+2，2﹣2）或（8﹣2，2+2），
∴A′（5+，﹣﹣1）或（5﹣，﹣1）．
综上所述，点A′的坐标为（3，1）、（+1，3﹣）、（1﹣，3+）、（5+，﹣﹣1）、（5﹣，﹣1）．
