题目内容
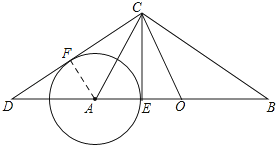
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.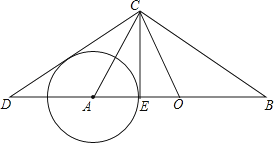
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD= ![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
【答案】
(1)
证明:∵∠ACB=∠DCO=90°,
∴∠ACB﹣∠ACO=∠DCO﹣∠ACO,
即∠ACD=∠OCB,
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=∠B,
∴∠ACD=∠B
(2)
解:(i)∵BC2=ABBE,
∴ ![]() ,
,
∵∠B=∠B,
∴△ABC∽△CBE,
∴∠ACB=∠CEB=90°,
∵∠ACD=∠B,
∴tan∠ACD=tan∠B= ![]() ,
,
设BE=4x,CE=3x,
由勾股定理可知:BE2+CE2=BC2,
∴(4x)2+(3x)2=100,
∴解得x=2 ![]() ,
,
∴CE=6 ![]() ;
;
(ii)过点A作AF⊥CD于点F,
∵∠CEB=90°,
∴∠B+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠B=∠ACE,
∵∠ACD=∠B,
∴∠ACD=∠ACE,
∴CA平分∠DCE,
∵AF⊥CE,AE⊥CE,
∴AF=AE,
∴直线CD与⊙A相切
【解析】(1)因为∠ACB=∠DCO=90°,所以∠ACD=∠OCB,又因为点O是Rt△ACB中斜边AB的中点,所以OC=OB,所以∠OCB=∠B,利用等量代换可知∠ACD=∠B;(2)(i)因为BC2=ABBE,所以△ABC∽△CBE,所以∠ACB=∠CEB=90°,因为tan∠ACD=tan∠B,利用勾股定理即可求出CE的值;
(ii)过点A作AF⊥CD于点F,易证∠DCA=∠ACE,所以CA是∠DCE的平分线,所以AF=AE,所以直线CD与⊙A相切.本题考查圆的综合问题,涉及等量代换,勾股定理,相似三角形的判定与性质,锐角三角函数等知识,知识点较综合,需要学生灵活运用所学知识解决问题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案