Question

【题目】如图，抛物线y＝x2＋bx＋c过点A(3，0)，B(1，0)，交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动(点P不与A重合)，过点P作PD∥y轴交直线AC于点D．

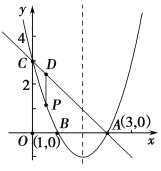
（1）求抛物线的解析式；

（2）求点P在运动的过程中线段PD长度的最大值；

（3）△APD能否构成直角三角形？若能，请直接写出所有符合条件的点P坐标；若不能，请说明理由．

Answer 1

【答案】（1）y＝x2-4x＋3；（2）点P在运动的过程中，线段PD长度的最大值为；（3）能，点P的坐标为：(1，0)或（2，-1）．

【解析】

（1）把点A、B的坐标代入抛物线解析式，解方程组得到b、c的值，即可得解；

（2）求出点C的坐标，再利用待定系数法求出直线AC的解析式，再根据抛物线解析式设出点P的坐标，然后表示出PD的长度，再根据二次函数的最值问题解答；

（3）分情况讨论①∠APD是直角时，点P与点B重合，②求出抛物线顶点坐标，然后判断出点P为在抛物线顶点时，∠PAD是直角，分别写出点P的坐标即可；

（1）把点A(3，0)和点B(1，0)代入抛物线y＝x2＋bx＋c，

得：

解得

∴y＝x2-4x＋3．

（2）把x＝0代入y＝x2-4x＋3，得y＝3．

∴C(0，3)．

又∵A(3，0)，

设直线AC的解析式为：y＝kx＋m，

把点A，C的坐标代入得：

∴直线AC的解析式为：y＝－x＋3．

PD＝-x＋3- (x2-4x＋3)＝-x2＋3x＝＋．

∵0<x<3，

∴x＝时，PD最大为．

即点P在运动的过程中，线段PD长度的最大值为．

（3）①∠APD是直角时，点P与点B重合，

此时，点P（1，0），

②∵y＝x2﹣4x+3＝（x﹣2）2﹣1，

∴抛物线的顶点坐标为（2，﹣1），

∵A（3，0），

∴点P为在抛物线顶点时，∠PAD＝45°+45°＝90°，

此时，点P（2，﹣1），

综上所述，点P（1，0）或（2，﹣1）时，△APD能构成直角三角形；