题目内容
如图,D,E分别是线段AB,AC上的点,BE与CD相交于点P.有如下三个关系式:①∠B=∠C;②AB=AC;③BE=CD.
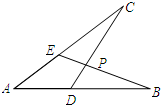
小题1:请你用其中两个关系式为条件,另一个为结论,写出一个你认为正确的命题:如果∠B=∠C,AB=AC ,那么BE=CD ;(不用序号表示)并证明。
小题2:以其中任意两个关系式为条件,另一个为结论构成真命题的概率是: 23.

小题1:请你用其中两个关系式为条件,另一个为结论,写出一个你认为正确的命题:如果∠B=∠C,AB=AC ,那么BE=CD ;(不用序号表示)并证明。
小题2:以其中任意两个关系式为条件,另一个为结论构成真命题的概率是: 23.
小题1:AB=AC,∠B=∠CBE=CD或∠B=∠C,BE=CD,AB=AC.(2分)
小题2:根据题意,各种组合有:
①已知∠B=∠C,AB=AC;求证:BE=CD.
证明:∵∠B=∠C,AB=AC,∠A=∠A,
∴△ACD≌△ABE,
∴BE=CD.
②已知:AB=AC,BE=CD;求证:∠B=∠C.
证明:∵AB=AC,BE=CD,∠A=∠A,
∴根据SSA,不能证明△ACD≌△ABE.
故不能证明:∠B=∠C.
③已知:∠B=∠C,BE=CD;求证:AB=AC.
证明:∵∠A=∠A,∠B=∠C,BE=CD,
∴△ACD≌△ABE.
∴AB=AC. (3分)
根据概率公式,P=
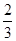 .(2分)
.(2分)(1)根据全等三角形的判定定理得出三角形全等,再由全等三角形的性质即可得出结论;
(2)根据题意写出所有命题,再得到所有真命题,根据概率公式即可解答.故答案为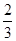 .
.
(2)根据题意写出所有命题,再得到所有真命题,根据概率公式即可解答.故答案为
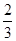 .
.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

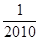 ,则密码位数至少需要 ◆ 位.
,则密码位数至少需要 ◆ 位.
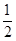 . (B)
. (B)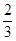 . (C)
. (C)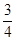 . (D)
. (D)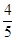 .
. 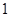 ,2,3,…20这二十个整数中任意取一个数,这个数是
,2,3,…20这二十个整数中任意取一个数,这个数是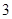 的倍数的概率是
的倍数的概率是