题目内容
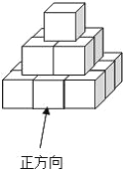
【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
【答案】(1)14;(2)4,1;(3)33cm2
【解析】
(1)该几何体中正方体的个数为最底层的9个,加上第二层的4个,再加上第三层的1个;(2)根据图中小正方体的位置解答即可;(3)涂上颜色部分的总面积可分上面,前面,后面,左面,右面,相加即可.
(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为:4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1![]() 1
1![]() 33=33cm2.
33=33cm2.

练习册系列答案
相关题目
【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖 | 二等奖 | 三等奖 |
1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
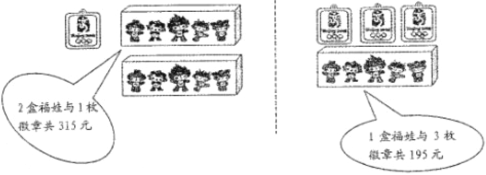
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?