题目内容
 如图,以△ABC的两条边为边长作两个正方形BDEC和ACFG,已知S△ABC:S四边形BDEC=2:7,正方形BDEC和正方形ACFG的边长之比为3:5,那么△CEF与整个图形面积的最简整数比是多少?
如图,以△ABC的两条边为边长作两个正方形BDEC和ACFG,已知S△ABC:S四边形BDEC=2:7,正方形BDEC和正方形ACFG的边长之比为3:5,那么△CEF与整个图形面积的最简整数比是多少?
解:∵△ABC的面积为 BC•AC•sin∠BCA,△CEF的面积为
BC•AC•sin∠BCA,△CEF的面积为 CE•CF•sin∠ECF,∠BCA+∠ECF=180°,
CE•CF•sin∠ECF,∠BCA+∠ECF=180°,
∴△ABC和△CEF的面积相等,
又 ,
,
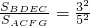 =
= ,
,
∴S△ABC:SBDEC:SACFG=18:63:175,
所求△CEF与整个图形面积的最简整数比为18:(18×2+63+175)=18:274=9:137.
分析:由题意得出三角形ABC和四边形BDEC的相似比,从而推出四边形BDEC与四边形ACFG的相似比,从而求解.
点评:此题主要考查了三角形的面积公式,用规则的图形表示出不规则的图形是解题的关键.
 BC•AC•sin∠BCA,△CEF的面积为
BC•AC•sin∠BCA,△CEF的面积为 CE•CF•sin∠ECF,∠BCA+∠ECF=180°,
CE•CF•sin∠ECF,∠BCA+∠ECF=180°,∴△ABC和△CEF的面积相等,
又
 ,
,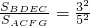 =
= ,
,∴S△ABC:SBDEC:SACFG=18:63:175,
所求△CEF与整个图形面积的最简整数比为18:(18×2+63+175)=18:274=9:137.
分析:由题意得出三角形ABC和四边形BDEC的相似比,从而推出四边形BDEC与四边形ACFG的相似比,从而求解.
点评:此题主要考查了三角形的面积公式,用规则的图形表示出不规则的图形是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
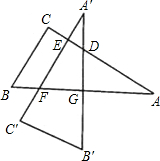 如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为
如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为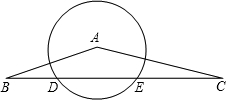 已知:如图,以△ABC的顶点A为圆心,r为半径的圆与边BC交于D、E两点,且AC2=CE•CB.
已知:如图,以△ABC的顶点A为圆心,r为半径的圆与边BC交于D、E两点,且AC2=CE•CB.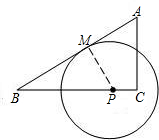
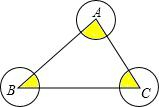 如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是
如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是