题目内容
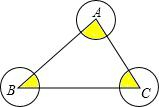如图，以△ABC的三顶点为圆心，半径为1，作两两不相交的扇形，则图中三个扇形面积之和是| 1 |
| 2 |
| 1 |
| 2 |
分析：根据三角形内角和定理得到三个扇形（图中阴影部分）的圆心角的和为180°，然后根据扇形的面积公式直接计算三个扇形面积之和．
解答：解：∵三个扇形（图中阴影部分）的圆心角的和为180°，
∴三个扇形面积之和=
=
π．
故答案为：
π．
∴三个扇形面积之和=
| 180π×12 |
| 360 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了三角形内角和定理和扇形面积的计算：扇形的面积公式为S=
（n为圆心角的度数，R为半径），解答此题的关键是沟通三角形内角与扇形的圆心角的关系，难度一般．
| nπR2 |
| 360 |
练习册系列答案
相关题目
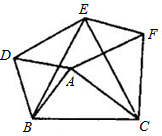25、如图，以△ABC的三边为边，在BC的同一侧分别作三个等边三角形，△ABD，△BCE和△ACF．
16、如图，以△ABC的三边为边，在BC的同侧分别另作三个等边三角形，即△ABD，△BCE，△ACF．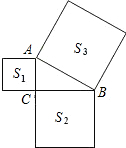
如图，以△ABC的各边为边分别向外作正方形，所得到的三个正方形的面积分别为S1=36，S2=64，S3=100，则△ABC的面积是（ ）
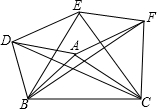如图，以△ABC的三边为边在BC的同一侧分别作三个等边三角形，即△ABD、△BCE、△ACF