Question

如图，Rt△ABC的两条直角边AC=3，BC=4，点P是边BC上的一动点（P不与B重合），以P为圆心作⊙P与BA相切于点M．设CP=x，⊙P的半径为y．
（1）求证：△BPM∽△BAC；
（2）求y与x的函数关系式，并确定当x在什么范围内取值时，⊙P与AC所在直线相离；
（3）当点P从点C向点B移动时，是否存在这样的⊙P，使得它与△ABC的外接圆相内切？若存在，求出x、y的值；若不存在，请说明理由．

Answer 1

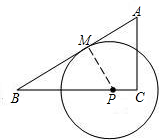
分析：（1）由∠B=∠B，∠C=∠BMP=90°证明；
（2）勾股定理求出AB的长，相似三角形求出y与x的函数关系式，求出取值范围；
（3）根据内切圆的特点，求出x，y的值．

解答：（1）证明：∵AB切⊙P于点M，
∴∠PMB=∠C=90°．
又∵∠B=∠B，
∴△BPM∽△BAC．

（2）解：∵AC=3，BC=4，∠C=90°，
∴AB=5．
∵

BP

BA

=

PM

AC

，
∴

4-x

5

=

y

3

，
∴y=-

3

5

x+

12

5

（0≤x＜4）．
当x＞y时，⊙P与AC所在的直线相离．
即x＞-

3

5

x+

12

5

，
得x＞

3

2

，
∴当

3

2

＜x＜4时，⊙P与AC所在的直线相离．

（3）解：设存在符合条件的⊙P．
得OP=2.5-y，而BM=

4

3

y，
∴OM=2.5-

4

3

y，
有(2.5-

4

3

y)2+y2=(2.5-y)2，
得

16

9

y2-

5

3

y=0
∴y₁=0（不合题意舍去），y₂=

15

16

．
∴y=

15

16

时，x=

39

16

．

点评：本题涉及的知识点较多，综合考查了相似三角形的应用和待定系数法求一次函数解析式．