Question

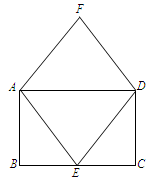
如图，正方形ABCD中，E、F均为中点，则下列结论中：①AF⊥DE； ②AD=BP； ③PE+PF=PC； ④PE+PF=PC。其中正确的是（　　）

A．①④      B．①②④      C．①③      D．①②③

Answer 1

D．

试题分析：如题图，
∵正方形ABCD，E，F均为中点，∴AD=DC=BC，∠ADC=∠DCB，EC=DF=DC.
∵在△ADF和△DCE中，AD＝DC，∠ADF＝∠DCE，DF＝CE，∴△ADF≌△DCE（SAS）.∴∠AFD=∠DEC.
∵∠DEC+∠CDE=90°，∴∠AFD+∠CDE=90°=∠DPF
∴AF⊥DE.∴①正确.
如图1，过B作BG∥DE交AD于G，交AP于M，
∵AF⊥DE，BG∥DE，E是BC中点，∴BG⊥AP，G是AD的中点.∴BG是AP的垂直平分线.
∴△ABP是等腰三角形.∴BP=AB=AD，∴②正确.
如图2，延长DE至N，使得EN=PF，连接CN，
∵∠AFD=∠DEC ，∴∠CEN=∠CFP.
又∵E，F分别是BC，DC的中点，∴CE=CF，
∵在△CEN和△CFP中，CE＝CF，∠CEN＝∠CFP，EN＝PF，∴△CEN≌△CFP（SAS）.∴CN=CP，∠ECN=∠PCF.
∵∠PCF+∠BCP=90°，∴∠ECN+∠BCP=∠NCP=90°.
∴△NCP是等腰直角三角形.∴PN=PE+NE=PE+PF=PC.∴③正确，④错误.
∴①②③正确．
故选D．