题目内容
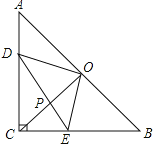
【题目】如图,抛物线y=a(x﹣1)2+k(a>0)经过点(﹣1,0),顶点为M,过点P(0,a+4)作x轴的平行线1,l与抛物线及其对称轴分别交于点A,B,H.以下结论:①当x=3.1时,y>0;②存在点P,使AP=PH;③(BP﹣AP)是定值;④设点M关于x轴的对称点为M',当a=2时,点M′在l下方,其中正确的是( )

A. ①③B. ②③C. ②④D. ①④
【答案】A
【解析】
根据二次函数的对称性可得抛物线与x轴的另一个交点的坐标为(3,0),且抛物线开口向上,可对①作判断;根据图形中与x轴交点坐标(-1,0)和对称轴与x轴交点(1,0)可对②作判断;根据对称性得:AH=BH,根据线段的和与差可对③作判断;根据M'的坐标和l到x轴的距离可对④作判断.
①由题意得:a>0,开口向上,
∵抛物线对称轴是x=1,且经过点(﹣1,0),
∴抛物线过x轴另一个点为(3,0),
∴当x=3.1时,y>0;
故①正确;
②当P在O点时,AP=PH,
∵a>0,
∴P不可能与O重合,
故②不正确;
③BP﹣AP=(BH+PH)﹣AP=AH+PH﹣AP=2PH=2,
故③正确;
④把(﹣1,0)代入y=a(x﹣1)2+k中,k=﹣4a,
当a=2时,a+4=6,﹣(﹣4a)=8,点M'在l的上方,
故④不正确;
所以正确的有:①③,
故选:A.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
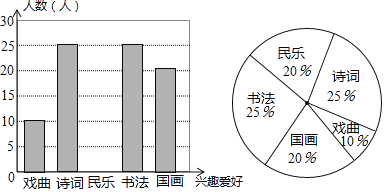
步步高口算题卡系列答案【题目】学校组织“校园诗词大会”,全校学生参加初赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩(满分100分),整理得到如下不完整的统计图表:
组别 | 成绩x分 | 频数(人数) | 频率 |
第1组 | 50≤x<60 | 6 | 0.12 |
第2组 | 60≤x<70 | 0.16 | |
第3组 | 70≤x<80 | 14 | a |
第4组 | 80≤x<90 | b | |
第5组 | 90≤x<100 | 10 |
请根据图表中所提供的信息回答下列问题:
(1)统计表中a= ,b= ;
(2)请将统计图表补充完整;
(3)根据调查结果,请估计该校1200名学生中,成绩不低于80分的人数.