题目内容
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
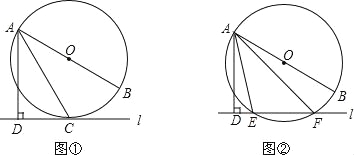
【答案】详见解析.
【解析】
试题分析:(1)连接OC,易得OC∥AD,根据平行线的性质就可以得到∠DAC=∠ACO,再根据OA=OC得到∠ACO=∠CAO,就可以证出结论;(2)如图②,连接BF,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,继而证得结论.
试题解析:(1)连接OC,
∵直线l与⊙O相切于点C,
∴OC⊥CD;
又∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO;
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)如图②,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=90°﹣∠B,
∴∠AEF=∠ADE+∠DAE,
在⊙O中,四边形ABFE是圆的内接四边形,
∴∠AEF+∠B=180°,
∴∠BAF=∠DAE.
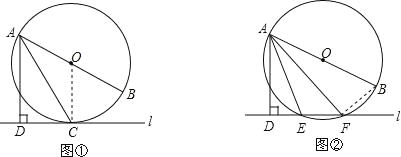

练习册系列答案
相关题目
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?