题目内容
【题目】如图1,已知在长方形ABCD中, AD=8, AB=4,将长方形ABCD沿着对角线BD折叠,使点C落在 ![]() 处,
处, ![]() 交AD于点E.
交AD于点E.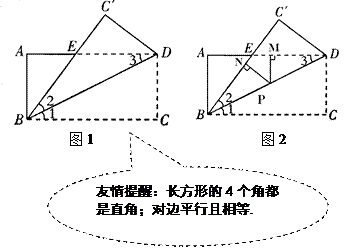
(1)求证:△BED是等腰三角形.
(2)求DE的长.
(3)如图2,若点P是BD上一动点, ![]() 于点N,
于点N, ![]() 于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
【答案】
(1)解:由翻折知,∠1=∠2 ,
∵AD∥BC,
∴∠3=∠2 ,
∴∠1=∠3,
∴BE=DE,
即△BED是等腰三角形
(2)解:设DE=x,则AE=8-x,BE=x,
在Rt△ABE中, ![]()
解之, x=5, ∴ DE=5
(3)解:PM+PN为定值,是4 ,
延长MP,交BC于点H,
∵AD∥BC,PM ![]() ,
,
∴PH⊥BC,
∵∠1=∠2, PN ![]() ,PH⊥BC,
,PH⊥BC,
∴PN=PH ,
∴ PM+PN=MN=AB=4
【解析】(1)根据折叠的性质,得到∠1=∠2 ,由AD∥BC,得到内错角相等得到∠3=∠2 ,即∠1=∠3,根据等角对等边得到BE=DE, 即△BED是等腰三角形;(2)在Rt△ABE中,根据勾股定理求出DE的长;(3)根据题意作出辅助线,得到PH⊥BC,再由∠1=∠2,得到PN=PH ,得到PM+PN=MN=AB的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?