题目内容
如图△ABC中,∠ACB=90°,AC=BC,AD是∠BAC的平分线,过D作DE⊥AB,垂足为E点.
(1)求证:AB=AC+CD;
(2)已知AC=4cm,求CD的长.
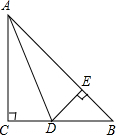
(1)求证:AB=AC+CD;
(2)已知AC=4cm,求CD的长.

(1)证明:∵AD是∠BAC的平分线,
∴∠CAD=∠EAD.
又∠AED=∠C=90°,AD=AD,
∴△ACD≌△AED.
∴AE=AC,DE=CD.
∵∠ACB=90°,AC=BC,
∴∠B=45°.
∴∠BDE=∠B=45°.
∴DE=BE,
∴AB=AE+BE=AC+CD.
(2)设CD=xcm,根据等腰直角三角形的性质,得BD=
xcm.
又AC=BC,
∴
x+x=4,
x=4
-4.
∴∠CAD=∠EAD.
又∠AED=∠C=90°,AD=AD,
∴△ACD≌△AED.
∴AE=AC,DE=CD.
∵∠ACB=90°,AC=BC,
∴∠B=45°.
∴∠BDE=∠B=45°.
∴DE=BE,
∴AB=AE+BE=AC+CD.
(2)设CD=xcm,根据等腰直角三角形的性质,得BD=
| 2 |
又AC=BC,
∴
| 2 |
x=4
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目