题目内容
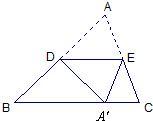（2007•海南）如图，△ABC沿DE折叠后，点A落在BC边上的A′处，若点D为AB边的中点，∠B=50°，则∠BDA′的度数为
80°
80°
．分析：由折叠的性质可知AD=A′D，再根据中点的性质得AD+BD，BD=A′D，∠DA′B=∠B=50°，从而求解∠BDA'的度数．
解答：解：由折叠的性质知，AD=A′D，
∵点D为AB边的中点
∴AD=BD，BD=A′D，∠DA′B=∠B=50°，
∴∠BDA′=180°-2∠B=80°．
∵点D为AB边的中点
∴AD=BD，BD=A′D，∠DA′B=∠B=50°，
∴∠BDA′=180°-2∠B=80°．
点评：本题利用了：1、折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；2、中点的性质，等边对等角，三角形的内角定理求解．
练习册系列答案
相关题目
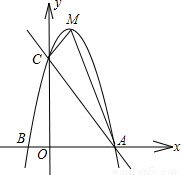
x+4与x轴交于点A，与y轴交于点C，已知二次函数的图象经过点A、C和点B（-1，0）．
个单位长度的速度沿折线OAC按O?A?C的路线运动，点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动，当D、E两点相遇时，它们都停止运动．设D、E同时从点O出发t秒时，△ODE的面积为S．
x+4与x轴交于点A，与y轴交于点C，已知二次函数的图象经过点A、C和点B（-1，0）．
个单位长度的速度沿折线OAC按O?A?C的路线运动，点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动，当D、E两点相遇时，它们都停止运动．设D、E同时从点O出发t秒时，△ODE的面积为S．
