题目内容
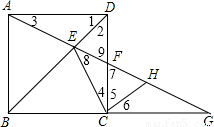
(2007•海南)如图,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.(1)求证:△ADE≌△CDE;
(2)过点C作CH⊥CE,交FG于点H,求证:FH=GH;
(3)设AD=1,DF=x,试问是否存在x的值,使△ECG为等腰三角形?若存在,请求出x的值;若不存在,请说明理由.

【答案】分析:(1)根据SAS可证△ADE≌△CDE;
(2)根据(1)的结论和图中各角的关系证明∠G=∠6,∠5=∠7即可;
(3)要使△ECG为等腰三角形,必须CE=CG,根据已知求得∠3的度数,再根据正切值进行计算求得.
解答:(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠1=∠2=45°,DE=DE,(3分)
∴△ADE≌△CDE.(4分)
(2)证明:∵△ADE≌△CDE,
∴∠3=∠4,
∵CH⊥CE,
∴∠4+∠5=90°,
又∵∠6+∠5=90°,
∴∠4=∠6=∠3,
∵AD∥BG,
∴∠G=∠3,
∴∠G=∠6,
∴CH=GH,(6分)
又∵∠G+∠5=∠G+∠7=90°,
∴∠5=∠7,
∴CH=FH,(7分)
∴FH=GH.(8分)
(3)解:存在符合条件的x值此时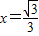 ,(10分)
,(10分)
∵∠ECG>90°,要使△ECG为等腰三角形,必须CE=CG,
∴∠G=∠8,
又∵∠G=∠4,
∴∠8=∠4,(11分)
∴∠9=2∠4=2∠3,
∴∠9+∠3=2∠3+∠3=90°,
∴∠3=30°,
∴x=DF=1×tan30°=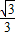 .(12分)
.(12分)
点评:此题综合性较强,主要考查了全等三角形的判定、三角形的内角和外角的性质、等腰三角形的判定.
(2)根据(1)的结论和图中各角的关系证明∠G=∠6,∠5=∠7即可;
(3)要使△ECG为等腰三角形,必须CE=CG,根据已知求得∠3的度数,再根据正切值进行计算求得.
解答:(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠1=∠2=45°,DE=DE,(3分)
∴△ADE≌△CDE.(4分)

(2)证明:∵△ADE≌△CDE,
∴∠3=∠4,
∵CH⊥CE,
∴∠4+∠5=90°,
又∵∠6+∠5=90°,
∴∠4=∠6=∠3,
∵AD∥BG,
∴∠G=∠3,
∴∠G=∠6,
∴CH=GH,(6分)
又∵∠G+∠5=∠G+∠7=90°,
∴∠5=∠7,
∴CH=FH,(7分)
∴FH=GH.(8分)
(3)解:存在符合条件的x值此时
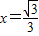 ,(10分)
,(10分)∵∠ECG>90°,要使△ECG为等腰三角形,必须CE=CG,
∴∠G=∠8,
又∵∠G=∠4,
∴∠8=∠4,(11分)
∴∠9=2∠4=2∠3,
∴∠9+∠3=2∠3+∠3=90°,
∴∠3=30°,
∴x=DF=1×tan30°=
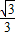 .(12分)
.(12分)点评:此题综合性较强,主要考查了全等三角形的判定、三角形的内角和外角的性质、等腰三角形的判定.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
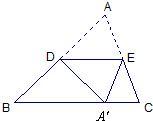 (2007•海南)如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为
(2007•海南)如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为
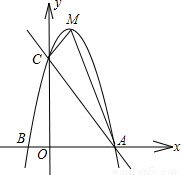
 x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).
x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0). 个单位长度的速度沿折线OAC按O?A?C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.
个单位长度的速度沿折线OAC按O?A?C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.
 x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).
x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0). 个单位长度的速度沿折线OAC按O?A?C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.
个单位长度的速度沿折线OAC按O?A?C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O?C?A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.