题目内容
【题目】如图,线段AB , AD交于点A . C为直线AD上一点(不与点A , D重合).过点C在BC的右侧作射线CE⊥BC , 过点D作直线DF∥AB , 交CE于点G(G与D不重合).
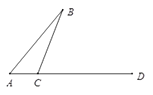
(1)如图1,若点C在线段AD上,且∠BCA为钝角.①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系;
(3)请你结合本题的题意提出一个新的拓展问题 .
【答案】
(1)
解:①补全图形如图

②判断:∠CGD-∠B=90°.
证明 :过点C作CH∥AB,
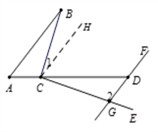
∴ ∠1=∠B(两直线平行,内错角相等).
∵ AB∥DF(已知),
∴ CH∥DF(平行于同一直线的两直线平行).
∴ ∠2+∠HCG=180°(两直线平行,同旁内角互补) .
∵ CE⊥BC(已知),
∴ ∠1+∠HCG=90°(垂直的定义).
∴ ∠CGD-∠B=90°
(2)∠CGD+∠B=90°
(3)若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?![]() 若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?![]() 若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
【解析】(1)①补全图形见解析;②先作辅助线,由∠2+∠HCG=180°和∠1+∠HCG=90°,推出结论∠CGD-∠B=90°即可;
(2)由(1)中②的结论可推导出结论∠CGD+∠B=90°. 附加题见解析.
(3)1.若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
2.若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
【考点精析】本题主要考查了垂线的性质和平行线的判定与性质的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.