题目内容
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
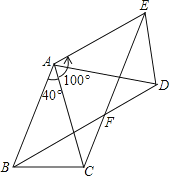
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形
【答案】(1)证明见解析;(2)40°;(3)证明见解析.
【解析】
试题分析:(1)根据旋转角求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等.
(2)根据全等三角形对应角相等,得出∠ACE=∠ABD,即可求得.
(3)根据对角相等的四边形是平行四边形,可证得四边形ABFE是平行四边形,然后依据邻边相等的平行四边形是菱形,即可证得.
试题解析:(1)∵△ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD与△ACE中

∴△ABD≌△ACE(SAS).
(2)∵∠CAE=100°,AC=AE,
∴∠ACE=![]() (180°-∠CAE)=
(180°-∠CAE)=![]() (180°-100°)=40°;
(180°-100°)=40°;
(3)∵∠BAD=∠CAE=100°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°-∠BAE-∠ABD-∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴平行四边形ABFE是菱形.

【题目】输入一组数据,按下列程序进行计算(x+8)2﹣826,输出结果如表:
x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
输出 | ﹣13.75 | ﹣8.04 | ﹣2.31 | 3.44 | 9.21 |
分析表格中的数据,估计方程(x+8)2﹣826=0的一个正数解x的大致范围为( )
A. 20.5<x<20.6 B. 20.6<x<20.7 C. 20.7<x<20.8 D. 20.8<x<20.9