题目内容
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①b＜0；②4a+2b+c＜0；③a﹣b+c＞0；④（a+c）2＜b2．其中正确的结论是（ ）
| A．①② | B．①③ | C．①③④ | D．①②③④ |
C
解析试题分析：①图象开口向上，对称轴在y轴右侧，能得到：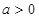
，
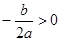，则
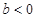，正确；
②∵对称轴为直线x=1，∴x=2与x=0时的函数值相等，∴当x=2时，y=4a+2b+c＞0，错误；
③当x=-1时，y=a-b+c＞0，正确；
④∵a-b+c＞0，∴a+c＞b；∵当x=1时，y=a+b+c＜0，∴a+c＜-b；∴b＜a+c＜-b，
∴|a+c|＜|b|，∴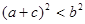
，正确．
所以正确的结论是①③④．
考点：二次函数的图象与系数的关系
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
或
.其中正确的是( )
若二次函数
配方后为
，则
、
的值分别为（ ）
| A．8、－1 | B．8、1 | C．6、－1 | D．6、1 |
，当x＞0时，y随x的增大而增大，则二次函数
的大致图象是（ ）
将二次函数y＝x2－2x＋3化为y＝(x－h)2＋k的形式结果为 ( )
| A．y＝(x＋1)2＋4 | B．y＝(x－1)2＋4 |
| C．y＝(x＋1)2＋2 | D．y＝(x－1)2＋2 |
抛物线y=2（x﹣3）2+1的顶点坐标是（ ）
| A．（3，1） | B．（3，﹣1） | C．（﹣3，1） | D．（﹣3，﹣1） |
抛物线
上部分点的横坐标ｘ，纵坐标y的对应值如下表：
| ｘ | … |  |  | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与ｘ轴的一个交点为
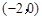②抛物线与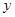
轴的交点为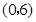
③抛物线的对称轴是：
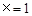④在对称轴左侧y随ｘ增大而增大A．1 Ｂ．2 Ｃ．3 Ｄ．4
中，当x＞0时，y随x的增大而增大，则二次函数
的图象大致是图中的（ ）
将抛物线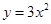
先向上平移3个单位，再向左平移2个单位后得到的抛物线解析式为（ ）
A． | B． |
C． | D． |